c 2pr формула что значит
C 2pr формула что значит
При движении по окружности с постоянной по величине линейной скоростью v тело испытывает направленное к центру окружности постоянное центростремительное ускорение
Вывод формулы для центростремительного ускорения
По определению
На рисунке треугольники, образованные векторами перемещений и скоростей, подобны. Учитывая, что |r1| = |r2| = R и |v1| = |v2| = v, из подобия треугольников находим:
откуда
Поместим начало координат в центр окружности и выберем плоскость, в которой лежит окружность, за плоскость (x, y). Положение точки на окружности в любой момент времени однозначно определяется полярным углом j, измеряемым в радианах (рад), причем
x = R cos(j + j0), y = R sin(j + j0),
где j0 определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).
В случае равномерного вращения угол j, измеряемый в радианах, линейно растет со временем:
Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью.
Зависимость координат точки на окружности от времени в случае равномерного вращения с заданной частотой можно записать в виде:
Время, за которое совершается один оборот, называется периодом T.
Связь циклической частоты с периодом и частотой: 2p = wT, откуда
Связь линейной скорости и угловой скорости находится из равенства: 2pR = vT, откуда
Выражение для центростремительного ускорения можно записать разными способами, используя связи между скоростью, частотой и периодом:
Связь поступательного и вращательного движений
Основные кинематические характеристики движения по прямой с постоянным ускорением: перемещение s, скорость v и ускорение a. Соответствующие характеристики при движении по окружности радиусом R: угловое перемещение j, угловая скорость w и угловое ускорение a (в случае, если тело вращается с переменной скоростью). Из геометрических соображений вытекают следующие связи между этими характеристиками:
Все формулы кинематики равноускоренного движения по прямой могут быть превращены в формулы кинематики вращения по окружности, если сделать указанные замены. Например:
s = vt
j = wt,
v = v0 + atw = w0 + at.
Связь между линейной и угловой скоростями точки при вращении по окружности можно записать в векторной форме. Действительно, пусть окружность с центром в начале координат расположена в плоскости (x, y). В любой момент времени вектор R, проведенный из начала координат в точку на окружности, где находится тело, перпендикулярен вектору скорости тела v, направленному по касательной к окружности в этой точке. Определим вектор w, который по модулю равен угловой скорости w и направлен вдоль оси вращения в сторону, которая определяется правилом правого винта: если завинчивать винт так, чтобы направление его вращения совпадало с направлением вращения точки по окружности, то направление движения винта показывает направление вектора w. Тогда связь трех взаимно перпендикулярных векторов R, v и w можно записать с помощью векторного произведения векторов:
2 Пи р квадрат это формула
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
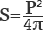
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Перевод радиан в градусы.
Ad = Ar * 180 / пи
Где Ad — угол в градусах, Ar — угол в радианах.
Перевод градусов в радианы.
Ar = Ad * пи / 180
Где Ad — угол в градусах, Ar — угол в радианах.
Длина окружности.
L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.
Длина дуги окружности.
L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах
Для окружности A = 2*пи (360 градусов), получим L = 2*пи*R.
Площадь треугольника.
S = (p * (p-a) * (p-b) * (p-c) ) 1/2
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.
Площадь круга.
S = пи * R 2
Где S — площадь круга, R — радиус круга.
Площадь сектора.
S = Ld * R/2 = (A * R 2 )/2
Где S — площадь сектора, R — радиус круга, Ld — длина дуги.
Площадь поверхности шара.
S = 4 * пи * R 2
Где S — площадь поверхности шара, R — радиус шара.
Площадь боковой поверхности цилиндра.
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь полной поверхности цилиндра.
S = 2 * пи * R * H + 2 * пи * R 2
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь боковой поверхности конуса.
S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
Площадь полной поверхности конуса.
S = пи * R * L + пи * R 2
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
Объем шара.
V = 4 / 3 * пи * R 3
Где V — объем шара, R — радиус шара.
Объем цилиндра.
V = пи * R 2 * H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Объем конуса.
V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.
Содержание
История [ править | править код ]
Использование многоугольников [ править | править код ]
Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус. [3]
Доказательство Архимеда [ править | править код ]
Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.
Не больше [ править | править код ]
Предположим, что площадь круга C больше площади треугольника T = 1 ⁄2cr. Пусть E означает превышение площади. Впишем [en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G4 больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G8. Продолжаем деление, пока общий зазор Gn не станет меньше E. Теперь площадь вписанного многоугольника Pn = C − Gn должна быть больше площади треугольника.
G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>>»> E = C − T > G n P n = C − G n > C − E P n > T E&<>=C-T\&<>>G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>> 
Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1 ⁄2nhs. Но h 1 ⁄2cr, получили противоречие.
Не меньше [ править | править код ]
Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G4 больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника Pn должна быть меньше T.
G_ \P_ &<>=C+G_ \&<> D = T − C > G n P n = C + G n C + D P n T =T-C\&<>>G_ \P_ &<>=C+G_ \&<> 
Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.
Таким образом, площадь круга в точности равна площади треугольника.
Доказательство перегруппировкой [ править | править код ]
| многоугольник | параллелограмм | |||
|---|---|---|---|---|
| n | сторона | основание | высота | площадь |
| 4 | 1,4142136 | 2,8284271 | 0,7071068 | 2,0000000 |
| 6 | 1,0000000 | 3,0000000 | 0,8660254 | 2,5980762 |
| 8 | 0,7653669 | 3,0614675 | 0,9238795 | 2,8284271 |
| 10 | 0,6180340 | 3,0901699 | 0,9510565 | 2,9389263 |
| 12 | 0,5176381 | 3,1058285 | 0,9659258 | 3,0000000 |
| 14 | 0,4450419 | 3,1152931 | 0,9749279 | 3,0371862 |
| 16 | 0,3901806 | 3,1214452 | 0,9807853 | 3,0614675 |
| 96 | 0,0654382 | 3,1410320 | 0,9994646 | 3,1393502 |
| ∞ | 1/∞ | π | 1 | π |
Интегрирование [ править | править код ]
Используя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2 π t dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.
Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:
Быстрая аппроксимация [ править | править код ]
Метод удвоения Архимеда [ править | править код ]
Если задан круг, пусть un будет периметром вписанного правильного n-угольника, а Un — периметром описанного правильного n-угольника. Тогда un и Un являются нижней и верхней границей длины окружности, которые становятся точнее с ростом n, а их среднее значение (un + Un)/2 становится особенно хорошей аппроксимацией длины окружности. Чтобы вычислить un и Un для больших n, Архимед вывел следующие формулы:
u 2 n = U 2 n u n = u_ >>> 

Начав с шестиугольника, Архимед удваивал n четыре раза, дойдя до 96-угольника, который дал ему хорошую аппроксимацию длины окружности круга.
В современных обозначениях можно воспроизвести эти вычисления (и пойти дальше). Для единичной окружности вписанный шестиугольник имеет периметр u6 = 6, а описанный шестиугольник имеет периметр U6 = 4√3. Удваиваем семь раз, получаем
Улучшение Снелла-Гюйгенса [ править | править код ]
Снелл предложил (а Гюйгенс доказал) более тесные границы, чем у Архимеда:
Для n = 48 формула даёт приближение лучше (около 3,14159292), чем метод Архимеда для n = 768.
Развитие формулы удваивания Архимеда [ править | править код ]
В первом равенстве отрезок C′P равен сумме C′O+OP, что равно r+ 1 ⁄2cn, а отрезок C′C является диаметром и его длина равна 2r. Для единичного круга получаем знаменитую формулу удвоения Людольфа Ван Цейлена
Если мы теперь построим правильный описанный n-угольник со стороной ″B″, параллельной AB, то OAB и OA″B″ являются подобными с отношением подобия A″B″ : AB = OC : OP. Обозначим описанную сторону Sn, тогда отношение превращается в Sn : sn = 1 : 1 ⁄2cn. (Мы снова используем факт, что OP равен половине A′B.) Получаем
Обозначим периметр вписанного многоугольника через un = nsn, а описанного через Un = nSn. Комбинируя равенства, получим
Можно также вывести
Аппроксимация случайными бросаниями [ править | править код ]
Конечная перегруппировка [ править | править код ]
Обобщения [ править | править код ]
Мы можем растянуть круг до формы эллипса. Поскольку это растяжение является линейным преобразованием плокости, оно изменяет площадь, но сохраняет отношения площадей. Этот факт можно использовать для вычисления площади произвольного эллипса, отталкиваясь от площади круга.
Пусть единичный эллипс описан квадратом со стороной 2. Преобразование переводит круг в эллипс путём сжатия или растяжения горизонтального и вертикального диаметров до малой и большой оси эллипса. Квадрат становится прямоугольником, описанным вокруг эллипса. Отношение площади круга к площади квадрата равно π /4, и отношение площади эллипса к площади прямоугольника будет тоже π /4. Если a и b — длины малой и большой осей эллипса. Площадь прямоугольника будет равна ab, а тогда площадь эллипса — π ab/4.
Мы можем распространить аналогичные техники и на большие размерности. Например, если мы хотим вычислить объём внутри сферы, и мы знаем формулу для площади сферы, мы можем использовать приём, аналогичный «луковичному» подходу для круга.
Коэффициент P/E простыми словами.
Значение цена — чистая прибыль позволяет быстро сравнить несколько абсолютно разных по капитализации компаний и сделать правильный выбор в пользу тех, которые в данный момент наиболее выгодные с точки зрения доходности.
Допустим у вас есть деньги и вы хотите купить квартиру (или несколько) для сдачи в аренду. Есть вариант квартиры с большой площадью стоимостью 100 000 долларов. Также можно на эти деньги купить 2 квартиры поменьше, по 50 тысяч каждая. Что же выбрать?
Исходя из этих данных получаем:
p/e большой квартиры будет равен 16,6 (100 000$ / (500$ х 12 мес.)
p/e маленькой квартиры будет равен 13,8 (50 000$ / (300$ х 12 мес.)
Исходя из полученного значения цена / чистая прибыль получаем, что покупка 2-х квартир более выгодное вложение. Ведь их срок окупаемости почти на 3 года меньше.
Соответственно обратное их p/e или доходность будет составлять 6% и 7,2%.
Тот же самый критерий можно применить и к оценке компаний. Возьмем самую популярную компанию Газпром. Стоимость самой компании (капитализация) составляет примерно 5423 миллиардов рублей, а сама компания заработала 1620 миллиардов чистой прибыли. В таком случае получаем:
P/E = 3,3 (5423 млрд. / 1620 млрд.)
Если вы купите всю компанию целиком, то сможете вернуть все потраченные деньги через 3,3 года. Конечно при условии, что норма прибыли не изменится.
Но так как вы скорее всего таких денег не имеете, то вам по карману купить только часть акций. Но прибыль, приходящаяся на одну акцию будет в той же пропорции, что и у всей компании. Поэтому P/E вашей инвестиции также будет 3,3.
Для компаний, акции которых торгуются на бирже, значение P/E будет зависеть от их котировок и нормы прибыли. Когда на рынке преобладает оптимизм — это толкает значение P/E вверх. Если пессимизм коэффициент цена — прибыль падает.
За последние 40 лет средний P/E акций, входящих в индекс S&P 500 составлял примерно 18. Причем в этот период наблюдались достаточно сильные отклонения как вверх так и вниз от среднего значения. Диапазон колебаний составлял от 10 до 35. Только на основании этих данных уже можно делать определенные выводы о дальнейших перспективах. Если значение выше 20 — это не самое лучшее время для покупки. А если соотношение цена прибыль достигает экстремальных значений 30-35 — самое время уходит с рынка и продавать все акции, так как идет явная переоцененность стоимости компаний.
Обычно высокие цены на акции обусловлены повышенными ожиданиями инвесторов роста доходов компании в будущем. В расчет берется бурный рост экономики, различные технологические изобретения, способные дать толчок компании. Конечно, это может повлиять на повышение прибыли, но на достаточно коротком интервале времени. Как правило, на долгосрочном периоде, размеры прибыли не сильно меняются. Поэтому излишний оптимизм по поводу роста дохода не оправдан.
Яркий пример опасности покупки акций при высоком P/E наблюдался в начале 2000-х в США во время бума IT-компаний. Все верили в то, что интернет-компании перевернут мир и их доходы будут со временем только расти. В то время котировки акций Yahoo достигали на бирже 100 долларов. При том, что прибыль на акцию составляла всего 12 центов. Коэффициент цена прибыль при этом составлял немыслимое число — 800. Это значило, чтобы окупить свои вложения при сохранении текущей прибыли нужно ждать 800 лет.
Конечно, никто не думал про это. Все считали, что компания будет наращивать прибыль, удваивая или утраивая ее с каждым годом. Но чуда не произошло. И вскоре котировки упали более чем в 20 раз.
Особенности использования P/E
Коэффициент позволяет практически на лету сравнивать компании, имеющие разные обороты, доходность, стоимость. Но следует понимать, что значение цена прибыль не дает полной картины и дополнительно у него есть ряд недостатков и особенностей, которые нужно учитывать проводя сравнительный анализ.
Вариантов как всегда несколько. Выбирайте понравившийся в зависимости от того, где вы торгуете и какие критерии отбора вам нужны.
«Расскажите мне 4P — маркетинга» — могут спросить на экзамене или собеседовании у будущего маркетолога. Но не так важно дать верный ответ, сколько понимать принцип работы этой концепции (читай — применять на практике). Об этом и будет наша статья. Инджой!
Вообще, теория 4P родилась ещё в 1964 году. Её придумал Нейл Борден и назвал «маркетинг-микс». Так что, если она актуальна столько времени, однозначно можно верить. Смысл был в том, что при составлении маркетингового плана, нужно обязательно учесть ряд составляющих. Продумать возможные негативные сценарии развития, затраты и тд. То есть, как Земля стоит на двух китах, маркетинг минимум на четырех:
Но, честно говоря, это сильно обобщенные понятия. В современной интерпретации концепции каждый элемент сам по себе содержит отдельный набор элементов. Рассмотрим каждую из P отдельно и подробно:
Здесь рассматривается именно товар или услуга, которые уже можно предложить своим клиентам (не прототип). Маркетолог изучает продукт от носа до хвоста — функционал, уникальность, плюсы и минусы, наличие гарантии/сопровождения/поддержки.
Зная все вышеперечисленное, он обращается к разным сегментам ЦА (целевая аудитория). Так как для разных категорий потребителей будут важны разные преимущества продукта.
В этот момент нужно посмотреть на товар с точки зрения задачи потребителя. Так покупатель хочет получить её решение, а не просто обладать продуктом. Подробнее о задачах и решения можно почитать в этой статье.
Допустим, Влад запустил новый сервис доставки. Алене — инструктору по йоге, следящей за своим питанием, будет важен ассортимент, наличие редких продуктов, суперфудов и тд. Насте — менеджеру высшего звена, скорость доставки. Потому что у неё совершенно нет времени ходить в магазин, а семья хочет быстро приготовленный ужин.
Таким образом, маркетолог нового сервиса понимает, что в упаковке/брендинге нужно делать акцент на скорости и разнообразии продуктов.
При составлении маркетингового плана эти знания могут помочь заложить в годовой бюджет деньги на ребрендинг логотипа/сайта или что-то подобное. Так как, возможно, нынешний брендинг не доносит до потребителя, что у сервиса действительно большой ассортимент и они быстро привозят заказы. Или, например, нужно переделать упаковку, чтобы она была более экологичной. Потому что компания недавно вступила в программу по сокращению пластика.
В итоге знания о продукте помогут собрать список необходимых действий, влияющих на общий маркетинговый план и его реализацию.
Конечно, в этом элементе имеется в виду ценообразование или ценовая политика компании. Этот пункт влияет на потребителя не только рационально, но и эмоционально. То есть, если цена гораздо ниже или выше средней по рынку, у покупателей могут появиться вопросы. Получается, что это пункт напрямую влияет на доверие.
Хотя, в первую очередь, от прайса зависит стратегия выхода на рынок. Есть несколько основных вариантов ценовых сегментов:
Возьмем в пример дорогой смартфон, лидер рынка. У него могут быть конкуренты, соответствующие по всем характеристикам, но с ценой на 20-30% ниже. Но большинство потребителей больше доверяют именно лидеру. Поэтому конкуренту нужен большой рекламный бюджет. Все эти вещи прописываются в маркетинговом плане, чтобы в дальнейшем найти более выгодный с точки зрения прибыли вариант.
Очень важный момент в пункте ценообразования — скидки, пакетные предложения, акции и тд. Здесь нужно просчитать возможности для разных сегментов сбыта.
Например, вы продаёте сливочный сыр в слайсах. Можете поставить скидку в зависимости от размера закупаемой продукции для дистрибьюторов, сформировать особые предложения и тд. Также на этом этапе определяются все условия возможных промо-мероприятий.
Вот мы и плавно перешли к 3 пункту — места сбыта товаров. Точнее к вопросу, как распространять товар. Эта часть включает всё от списка точек продаж до логистики и учета, сколько товара нужно хранить на складе.
Для компании продающих именно товары — это конкретные места продаж: магазины, кафе и тд. Для услуг местами могут считаться размещения на разных агрегаторах. Например, для доставок есть сервисы Delivery Club, Яндекс.Еда.
Также мы продумываем географию, выгоду продаж в другие города или страны. Считаем, во сколько будет обходиться логистика и выгодно ли это. Для точек продаж нужно продумать правила выкладки и её количество. Прописать условия хранения и даже предусмотреть проверки и штрафы, если договоренности не выполняются.
Этот пункт — раздолье для маркетологов. Сюда входят все маркетинговые коммуникации, реклама, PR и тд. Этими инструментами маркетологи могут реализовывать или скорректировать образ продукта, его восприятие на рынке.
Также с помощью продвижения есть возможность создать спрос на продукт. Случай, когда вы сделали крутой стартап, но потребители пока не знают, что ваш продукт им нужен. В свое время так было с ноутбуками, смартфонами и тд.
Ещё важный момент — коммуникация, направленная на удержание клиента. То есть возврат и повторная покупка. Тут подключается ремаркетинг, имиджевая реклама и прочее.
В общем, проще говоря, эта P отвечает за составления плана продвижения: формирование бюджета, постановка конкретных целей и задач (увеличить количество новых клиентов в 2 раза к 2021 году), выбор коммуникационных каналов, продумывание возможных ивентов. Здесь же уже более конкретно прописывается план рекламных акций, скидок и тд.
Выше мы рассмотрели самый классический вариант модели 4P. Но с годами она неоднократно модифицировалась и расширялась до 5, 7, 10P.
Сама суть не поменялась, но выявились акценты, на которые точно нужно обратить внимание при составлении маркетингового плана. Для каждого товара/услуги выбирается наиболее подходящий вариант. Жестких правил здесь, конечно, нет.
Какие еще P могут добавляться:
В действительности, дополнительных пунктов может быть ещё больше, но мы решили показать наиболее важные. Помните, что в любом случае, маркетинг — гибкая наука, которая ежесекундно подстраивается под изменения рынка. Поэтому не бойтесь пробовать отходить от теорий, хотя и стоит полагаться на их опыт.
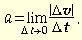
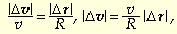
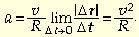
 j = wt,
j = wt, 







