csc что такое в математике

Документация

Косеканс входного угла в радианах

Синтаксис

Описание

Примеры

Графическое изображение функции косеканса

Косеканс вектора комплексных углов

Входные параметры

X — Введите угол в радианах
скаляр | вектор | матрица | многомерный массив

Введите угол в радианах в виде скаляра, вектора, матрицы или многомерного массива.

Типы данных: single | double
Поддержка комплексного числа: Да

Выходные аргументы

Y — Косеканс входного угла
скаляр | вектор | матрица | многомерный массив

Косеканс входного угла, возвращенного как скаляр с комплексным знаком или с действительным знаком, вектор, матричный или многомерный массив.

Больше о

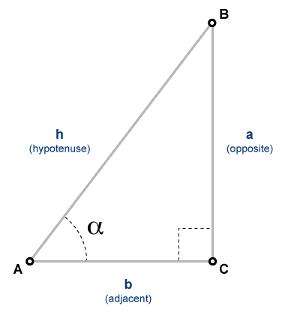
Функция косеканса

Косеканс угла, α, заданный со ссылкой на право повернул, треугольник

Косеканс сложного аргумента, α,

Советы

Расширенные возможности

«Высокие» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Смотрите также

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Документация MATLAB

Поддержка

© 1994-2021 The MathWorks, Inc.

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Источник

13. Тригонометрические функции

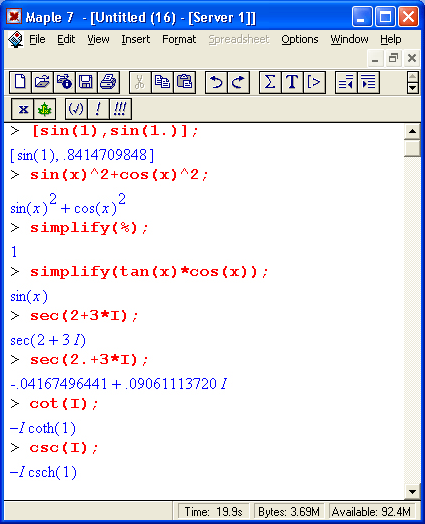
В ядре Maple определены следующие тригонометрические функции:

Все эти функции являются периодическими (с периодом 2л, кроме тангенса и котангенса, у которых период равен л) и определены для действительного и комплексного аргументов. Примеры вычислений:

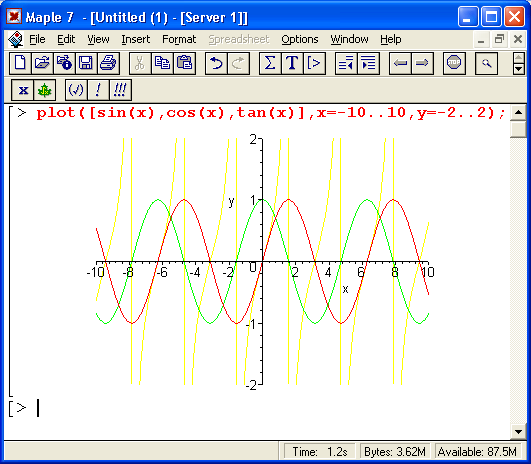
Многие свойства тригонометрических функций можно оценить, рассматривая их графики. Для построения таких графиков можно использовать функцию pi ot. На рис. 6.1 сверху показаны графики ряда тригонометрических функций.

Рис. 6.1. Графики ряда тригонометрических и обратных тригонометрических функций

Из графиков тригонометрических функций (рис. 6.1, сверху) хорошо видна их периодичность. Функция тангенса имеет разрывы, и ее значение в этих точках в пределе равно бесконечности. Поэтому для наглядного ее представления вместе с функциями синуса и косинуса (их экстремальные значения по модулю равны 1) приходится вводить ограничения на масштаб графика по оси у.

Обратите внимание на параметр color=black в функции построения графиков plot. Он задает построение всех графиков черным цветом, что сделано для более четкой печати их в книге. Если убрать этот параметр, то графики разных функций будут строиться с использованием разных цветов, что облегчит их различение. Другие способы выделения отдельных кривых будут описаны в дальнейшем при описании графических возможностей системы Maple 7.

Источник

Как легко понять знаки Σ и П с помощью программирования

Для тех, кто подзабыл матешу

Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.

Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.

Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.

Знак Σ — сумма

Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:

Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.

На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:

Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».

Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:

Произведение П

С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:

А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:

Что дальше

Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.

Источник

Csc что такое в математике

1 CSC

2 CSC

Международная конвенция о безопасной перевозке грузов в контейнерах (ООН)
—
[[Англо-русский словарь сокращений транспортно-экспедиторских и коммерческих терминов и выражений ФИАТА]]

Тематики

опорный цилиндр активной зоны ядерного реактора
—
[А.С.Гольдберг. Англо-русский энергетический словарь. 2006 г.]

Тематики

Тематики

плата за услуги, связанные с контейнерными перевозками
—
[[Англо-русский словарь сокращений транспортно-экспедиторских и коммерческих терминов и выражений ФИАТА]]

Тематики

Центр по техническому обслуживанию камер сгорания газовых турбин
(фирмы «Дженерал Электрик»)
[А.С.Гольдберг. Англо-русский энергетический словарь. 2006 г.]

Тематики

3 CSC

4 csc

5 CSC

6 CSC

7 CSC

8 CSC

9 csc

10 CSC

11 CSC

12 CSC

13 CSC

14 CSC

15 CSC

16 CSC

17 CSC

18 .CSC

19 CSC

См. также в других словарях:

CSC — CSC, Csc or CSc is a three letter acronym and may refer to: Contents 1 Awards 2 Science and industry 3 Companies and organizations 4 Other … Wikipedia

CSC — Abreviatura de centro de salud comunitario. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A. 1999 … Diccionario médico

CSC — Civil Service Commission Short Dictionary of (mostly American) Legal Terms and Abbreviations … Law dictionary

CSC — sigla Centro Sperimentale di Cinematografia … Dizionario italiano

CSC — abbrev. 1. Civil Service Commission 2. [L Congregatio a Sancta Cruce] Congregation of the Holy Cross … English World dictionary

csc — abbrev. Trigonometry cosecant … English World dictionary

CSC — Die Abkürzung CSC steht für: Centro Sperimentale di Cinematografia, Experimentelles Zentrum für Kinematographie in Rom Combat Survival Course, einen Überlebenslehrgang der Bundeswehr Computer Sciences Corporation, einen Informationsdienstleister… … Deutsch Wikipedia

Csc — Die Abkürzung CSC steht für Überlebenslehrgang der Bundeswehr Combat Survival Course den Informationsdienstleister Computer Sciences Corporation das von der Computer Sciences Corporation gesponserte dänische Radsport Team Team CSC den… … Deutsch Wikipedia

CSC — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sigles d’une seule lettre Sigles de deux lettres > Sigles de trois lettres Sigles de quatre lettres … Wikipédia en Français

csc — abbr. 1 Civil Service Commission. 2 Conspicuous Service Cross. * * * abbreviation cosecant * * * Civil Service Commission. * * * abbrev Civil Service Commission * * * csc (no periods), cosecant. CSC (no periods), Civil Service Commission. C.S.C … Useful english dictionary

CSC — • Computer Science(s) Corporation, seit 1959 (USA) • Circuit Switching Center • Civil Service Commission, USA • Common Signalling Channel • Computer Society of Canada • Construction Specifications Canada • Castleton State College, Vermont… … Acronyms

Источник

Что такое csc в математике

Ввод чисел:

Ввод переменных и констант:

Сумма и разность:

Умножение:

Деление:

Степень:

Приоритет операций:

Ввод функций:

В систему MATLAB встроены все основные элементарные математические функции, которые представлены в таблице 1.1.4. Вместе с тем, следует отметить, что список функций, приведенный в данном пункте, составляет лишь крохотную часть всего набора библиотечных функций, встроенных в MATLAB.

Таблица 1.4. Основные элементарные математические функции.

Не нашли то, что искали? Воспользуйтесь поиском:

e — основание натурального логарифма с приближенным числовым значением 2.71828.
pi — число, имеющее значение 3.14159. и равное отношению длины окружности к ее диаметру
i — представляет мнимую единицу, sqrt(-1)
Degree — число радиан в одном градусе, которое имеет числовое значение pi/180
EulerGamma — постоянная Эйлера с числовым значением 0.577216.
GoldenRatio — константа со значением (1+sqrt(5))/2, определяющая деление отрезка по правилу золотого сечения

Элементарные функции:
abs(x) — модуль значения x, |x|
sqrt(x) — квадратный корень значения x, √x
x^y — x в степени y, x y
e^x=exp(x) — экспонента значения x, e x
log(a,b) — логарифм значения b по основанию a, Log_a(b)
log(x) — натуральный логарифм значения x, Log_e(x)
dilog(x) — дилогарифм значения x, Li₂(x)
n! — факториал числа n, равный n×(n-1)×. ×3×2×1, причем 0!=1 и 1!=1
n!! — двойной факториал числа n, равный n×(n-2)×(n-4)×.

Тригонометрические функции:
sin(x) — синус значения x
cos(x) — косинус значения x
tan(x) — тангенс значения x
cot(x) — котангенс значения x
sec(x) — секанс значения x, sec(x)=1/cos(x)
csc(x) — косеканс значения x, csc(x)=1/sin(x)

Обратные тригонометрические функции:
arcsin(x) — арксинус значения x, sin -1 (x)
arccos(x) — арккосинус значения x, cos -1 (x)
arctan(x) — арктангенс значения x, tan -1 (x)
arccot(x) — арккотангенс значения x, cot -1 (x)
arcsec(x) — арксеканс значения x, sec -1 (x)
arccsc(x) — арккосеканс значения x, csc -1 (x)

Гиперболические функции:
sinh(x) — синус гиперболический значения x
cosh(x) — косинус гиперболический значения x
tanh(x) — тангенс гиперболический значения x
coth(x) — котангенc гиперболический значения x
sech(x) — секанс гиперболический значения x
csch(x) — косеканс гиперболический значения x

Обратные гиперболические функции:
arcsinh(x) — арксинус гиперболический значения x, sinh -1 (x)
arccosh(x) — арккосинус гиперболический значения x, cosh -1 (x)
arctanh(x) — арктангенс гиперболический значения x, tanh -1 (x)
arccoth(x) — арккотангенc гиперболический значения x, coth -1 (x)
arcsech(x) — арксеканс гиперболический значения x, sech -1 (x)
arccsch(x) — арккосеканс гиперболический значения x, csch -1 (x)

Функции комплексного аргумента:
abs(z) — модуль комплексного числа z
arg(z) — аргумент комплексного числа z
Im(z) — мнимая часть комплексного числа z
Re(z) — вещественная часть комплексного числа z

Ортогональные многочлены:
ChebyshevT(n,x) — полином Чебышева n-й степени первого рода, T_n(x)
ChebyshevU(n,x) — полином Чебышева n-й степени второго рода, U_n(x)
HermiteH(n,x) — полином Эрмита n-й степени, H_n(x)
JacobiP(n,a,b,x) — полином Якоби n-й степени, P_n (a,b) (x)
GegenbauerC(n,m,x) — полином Гегенбауэра, C_n (m) (x)
LaguerreL(n,x) — полином Лагерра n-й степени, L_n(x)
LaguerreL(n,a,x) — обобщенный полином Лагерра n-й степени, L_n a (x)
LegendreP(n,x) — полином Лежандра n-й степени, P_n(x)
LegendreP(n,m,x) — присоединенный полином Лежандра, P_n m (x)
LegendreQ(n,x) — функция Лежандра второго рода n-го порядка, Q_n(x)
LegendreQ(n,m,x) — присоединенная функция Лежандра второго рода, Q_n m (x)

Интегральные показательные и родственные им функции:
SinIntegral(x) — интегральный синус, Si(x)
SinhIntegral(x) — интегральный гиперболический синус, Shi(x)
CosIntegral(x) — интегральный косинус, Сi(х)
CoshIntegral(x) — интегральный гиперболический косинус, Сhi(х)
ExpIntegralEi(x) — интегральная показательная функция, Ei(x)
ExpIntegralE(n,x) — интегральная показательная функция, E_n(x)
FresnelC(x) — интеграл Френеля, C(x)
FresnelS(x) — интеграл Френеля, S(x)
li(x) — интегральный логарифм
erf(x) — функция ошибок (интеграл вероятности)
erf(x0,x1) — обобщенная функция ошибок, erf(x₁)-erf(x )
erfc(x) — дополняющая функция ошибок, 1-erf(x)
erfi(x) — мнимое значение функции ошибок, erfi(i×x)/i

Гамма- и полигамма-функции:
Gamma(x) — эйлерова гамма-функция, Γ(x)
Gamma(a,x) — неполная гамма-функция, Γ(a,x)
Gamma(a,x0,x1) — обобщенная неполная гамма-функция, Γ(а,x )-Γ(a,x₁)
GammaRegularized(a,x) — регуляризованная неполная гамма-функция, Q(а,x)=Γ(а,x)/Γ(a)
GammaRegularized(a,x0,x1) — обобщенная неполная гамма-функция, Q(a,x )-Q(a,x₁)
LogGamma(x) — логарифм эйлеровой гамма-функции, logΓ(x)
PolyGamma(x) — дигамма-функция, ψ(x)
PolyGamma(n,x) — n-я производная от дигамма-функции, ψ (n) (x)

Функции Бесселя:
BesselJ(n,x) — функция Бесселя первого рода, J_n(x)
BesselI(n,x) — модифицированная функция Бесселя первого рода, I_n(x)
BesselY(n,x) — функция Бесселя второго рода, Y_n(x)
BesselK(n,x) — модифицированная функция Бесселя второго рода, К_n(x)

Гипергеометрические функции:
Hypergeometric0F1(a,x) — гипергеометрическая функция, F₁(;a;x)
Hypergeometric0F1Regularized(a,x) — регуляризованная гипергеометрическая функция, F₁(;a;x)/Γ(a)
Hypergeometric1F1(a,b,x) — вырожденная гипергеометрическая функция Куммера, ₁F₁(;a;b;x)
Hypergeometric1F1Regularized(a,b,x) — регуляризованная вырожденная гипергеометрическая функция, ₁F₁(;a;b;x)/Γ(b)
HypergeometricU(a,b,x) — конфлюэнтная (вырожденная) гипергеометрическая функция, U(a,b,x)
Hypergeometric2F1(a,b,c,x) — гипергеометрическая функция ₂F₁(a,b;c;x)
Hypergeometric2F1Regularized(a,b,c,x) — регуляризованная гипергеометрическая функция ₂F₁(a,b;c;x)/Γ(c)

Эллиптические интегралы:
EllipticK(m) — полный эллиптический интеграл первого рода, К(m)
EllipticF(x,m) — эллиптический интеграл первого рода, F(x|m)
EllipticE(m) — полный эллиптический интеграл второго рода, Е(m)
EllipticE(x,m) — эллиптический интеграл второго рода Е(x|m)
EllipticPi(n,m) — полный эллиптический интеграл третьего рода, Π(n|m)
EllipticPi(n,x,m) — эллиптический интеграл третьего рода, Π(n;x|m)
JacobiZeta(x,m) — дзета-функция Якоби, Z(x|m)

Эллиптические функции:
am(x,m) — амплитуда для эллиптических функций Якоби, am(x|m)
JacobiSN(x,m) — эллиптическая функция Якоби, sn(x|m)
JacobiSD(x,m) — эллиптическая функция Якоби, sd(x|m)
JacobiSC(x,m) — эллиптическая функция Якоби, sc(x|m)
JacobiNS(x,m) — эллиптическая функция Якоби, ns(x|m)
JacobiND(x,m) — эллиптическая функция Якоби, nd(x|m)
JacobiNC(x,m) — эллиптическая функция Якоби, nc(x|m)
JacobiDS(x,m) — эллиптическая функция Якоби, ds(x|m)
JacobiDN(x,m) — эллиптическая функция Якоби, dn(x|m)
JacobiDC(x,m) — эллиптическая функция Якоби, dc(x|m)
JacobiCS(x,m) — эллиптическая функция Якоби, cs(x|m)
JacobiCN(x,m) — эллиптическая функция Якоби, cn(x|m)
JacobiCD(x,m) — эллиптическая функция Якоби, cd(x|m)
InverseJacobiSN(x,m) — обратная эллиптическая функция Якоби, sn -1 (x|m)
InverseJacobiSD(x,m) — обратная эллиптическая функция Якоби, sd -1 (x|m)
InverseJacobiSC(x,m) — обратная эллиптическая функция Якоби, sc -1 (x|m)
InverseJacobiNS(x,m) — обратная эллиптическая функция Якоби, ns -1 (x|m)
InverseJacobiND(x,m) — обратная эллиптическая функция Якоби, nd -1 (x|m)
InverseJacobiNC(x,m) — обратная эллиптическая функция Якоби, nc -1 (x|m)
InverseJacobiDS(x,m) — обратная эллиптическая функция Якоби, ds -1 (x|m)
InverseJacobiDN(x,m) — обратная эллиптическая функция Якоби, dn -1 (x|m)
InverseJacobiDC(x,m) — обратная эллиптическая функция Якоби, dc -1 (x|m)
InverseJacobiCS(x,m) — обратная эллиптическая функция Якоби, cs -1 (x|m)
InverseJacobiCN(x,m) — обратная эллиптическая функция Якоби, cn -1 (x|m)
InverseJacobiCD(x,m) — обратная эллиптическая функция Якоби, cd -1 (x|m)

Источник