integer division or modulo by zero что значит
Значения исключений и ошибок в Python
Обработка ошибок увеличивает отказоустойчивость кода, защищая его от потенциальных сбоев, которые могут привести к преждевременному завершению работы.
Прежде чем переходить к обсуждению того, почему обработка исключений так важна, и рассматривать встроенные в Python исключения, важно понять, что есть тонкая грань между понятиями ошибки и исключения.
Обработка исключений делает код более отказоустойчивым и помогает предотвращать потенциальные проблемы, которые могут привести к преждевременной остановке выполнения. Представьте код, который готов к развертыванию, но все равно прекращает работу из-за исключения. Клиент такой не примет, поэтому стоит заранее обработать конкретные исключения, чтобы избежать неразберихи.
Ошибки могут быть разных видов:
Разберем их по очереди.
Синтаксические ошибки (SyntaxError)
Синтаксические ошибки часто называют ошибками разбора. Они возникают, когда интерпретатор обнаруживает синтаксическую проблему в коде.
Рассмотрим на примере.
Стрелка вверху указывает на место, где интерпретатор получил ошибку при попытке исполнения. Знак перед стрелкой указывает на причину проблемы. Для устранения таких фундаментальных ошибок Python будет делать большую часть работы за программиста, выводя название файла и номер строки, где была обнаружена ошибка.
Недостаточно памяти (OutofMemoryError)
Но поскольку Python использует архитектуру управления памятью из языка C (функция malloc() ), не факт, что все процессы восстановятся — в некоторых случаях MemoryError приведет к остановке. Следовательно, обрабатывать такие ошибки не рекомендуется, и это не считается хорошей практикой.
Ошибка рекурсии (RecursionError)
Эта ошибка связана со стеком и происходит при вызове функций. Как и предполагает название, ошибка рекурсии возникает, когда внутри друг друга исполняется много методов (один из которых — с бесконечной рекурсией), но это ограничено размером стека.
Все локальные переменные и методы размещаются в стеке. Для каждого вызова метода создается стековый кадр (фрейм), внутрь которого помещаются данные переменной или результат вызова метода. Когда исполнение метода завершается, его элемент удаляется.
Ошибка отступа (IndentationError)
Эта ошибка похожа по духу на синтаксическую и является ее подвидом. Тем не менее она возникает только в случае проблем с отступами.
Исключения
Даже если синтаксис в инструкции или само выражение верны, они все равно могут вызывать ошибки при исполнении. Исключения Python — это ошибки, обнаруживаемые при исполнении, но не являющиеся критическими. Скоро вы узнаете, как справляться с ними в программах Python. Объект исключения создается при вызове исключения Python. Если скрипт не обрабатывает исключение явно, программа будет остановлена принудительно.
Программы обычно не обрабатывают исключения, что приводит к подобным сообщениям об ошибке:
Ошибка типа (TypeError)
Ошибка деления на ноль (ZeroDivisionError)
Оставшаяся часть строки с ошибкой предлагает подробности о причине ошибки на основе ее типа.
Теперь рассмотрим встроенные исключения Python.
Встроенные исключения
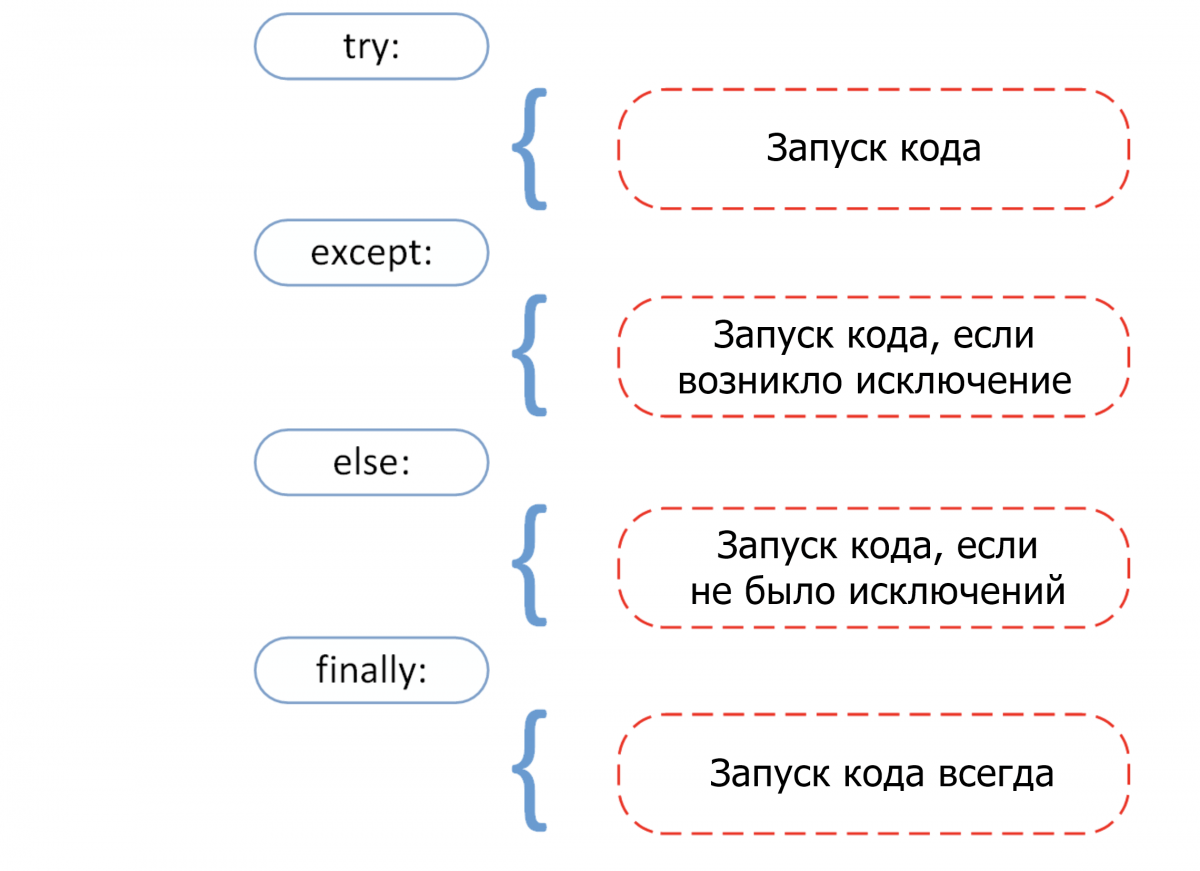
Прежде чем переходить к разбору встроенных исключений быстро вспомним 4 основных компонента обработки исключения, как показано на этой схеме.
В следующем разделе руководства больше узнаете об общих типах исключений и научитесь обрабатывать их с помощью инструмента обработки исключения.
Ошибка прерывания с клавиатуры (KeyboardInterrupt)
Исключение KeyboardInterrupt вызывается при попытке остановить программу с помощью сочетания Ctrl + C или Ctrl + Z в командной строке или ядре в Jupyter Notebook. Иногда это происходит неумышленно и подобная обработка поможет избежать подобных ситуаций.
Стандартные ошибки (StandardError)
Рассмотрим некоторые базовые ошибки в программировании.
Арифметические ошибки (ArithmeticError)
Все перечисленные выше исключения относятся к классу Arithmetic и вызываются при ошибках в арифметических операциях.
Деление на ноль (ZeroDivisionError)
Когда делитель (второй аргумент операции деления) или знаменатель равны нулю, тогда результатом будет ошибка деления на ноль.
Переполнение (OverflowError)
Ошибка переполнение вызывается, когда результат операции выходил за пределы диапазона. Она характерна для целых чисел вне диапазона.
Ошибка утверждения (AssertionError)
Когда инструкция утверждения не верна, вызывается ошибка утверждения.
Ошибка атрибута (AttributeError)
Ошибка импорта (ModuleNotFoundError)
Ошибка импорта вызывается при попытке импортировать несуществующий (или неспособный загрузиться) модуль в стандартном пути или даже при допущенной ошибке в имени.
Ошибка поиска (LookupError)
LockupError выступает базовым классом для исключений, которые происходят, когда key или index используются для связывания или последовательность списка/словаря неверна или не существует.
Здесь есть два вида исключений:
Ошибка ключа
Ошибка индекса
Если пытаться получить доступ к индексу (последовательности) списка, которого не существует в этом списке или находится вне его диапазона, будет вызвана ошибка индекса (IndexError: list index out of range python).
Ошибка памяти (MemoryError)
Как уже упоминалось, ошибка памяти вызывается, когда операции не хватает памяти для выполнения.
Ошибка имени (NameError)
Ошибка имени возникает, когда локальное или глобальное имя не находится.
Ошибка выполнения (Runtime Error)
Ошибка типа (TypeError)
Ошибка типа вызывается при попытке объединить два несовместимых операнда или объекта.
В примере ниже целое число пытаются добавить к строке, что приводит к ошибке типа.
Ошибка значения (ValueError)
Ошибка значения вызывается, когда встроенная операция или функция получают аргумент с корректным типом, но недопустимым значением.
В этом примере встроенная операция float получат аргумент, представляющий собой последовательность символов (значение), что является недопустимым значением для типа: число с плавающей точкой.
Пользовательские исключения в Python
В Python есть много встроенных исключений для использования в программе. Но иногда нужно создавать собственные со своими сообщениями для конкретных целей.
Это можно сделать, создав новый класс, который будет наследовать из класса Exception в Python.
В предыдущем примере если ввести что-либо меньше 1, будет вызвано исключение. Многие стандартные исключения имеют собственные исключения, которые вызываются при возникновении проблем в работе их функций.
Недостатки обработки исключений в Python
У использования исключений есть свои побочные эффекты, как, например, то, что программы с блоками try-except работают медленнее, а количество кода возрастает.
Поэтому стоит ограничить использование обработки исключений в Python и применять его в редких случаях. Например, когда вы не уверены, что будет вводом: целое или число с плавающей точкой, или не уверены, существует ли файл, который нужно открыть.
Выводы!
Как вы могли увидеть, обработка исключений помогает прервать типичный поток программы с помощью специального механизма, который делает код более отказоустойчивым.
Обработка исключений — один из основных факторов, который делает код готовым к развертыванию. Это простая концепция, построенная всего на 4 блоках: try выискивает исключения, а except их обрабатывает.
Очень важно поупражняться в их использовании, чтобы сделать свой код более отказоустойчивым.
Обработка исключений в Python
Что вы предпринимаете, когда с работой вашей программы что-то идет не так? Допустим, вы пытаетесь открыть файл, но вы ввели неверный путь, или вы хотите узнать информацию у пользователей и они пишут какую-то бессмыслицу. Вы не хотите, чтобы ваша программа крэшилась, по-этому вы выполняете обработку исключений. В Пайтоне, конструкция всегда обернута в то, что называется try/except. В данном разделе мы рассмотрим следующие понятия:
Начнем со знакомства с самыми обычными исключениями, которые вы увидите в Пайтоне. Обратите внимание на то, что ошибка и исключение – два разных слова, описывающие одно и то же, в контексте обработки исключений.
Основные исключения
Вы уже сталкивались со множеством исключений. Ниже изложен список основных встроенных исключений (определение в документации к Пайтону):
Существует много других исключений, но вы вряд ли будете сталкиваться с ними так же часто. В целом, если вы заинтересованы, вы можете узнать больше о них в документации Пайтон.
Как обрабатывать исключения?
Обработка исключений в Пайтон – это очень просто. Потратим немного времени и напишем несколько примеров, которые их вызовут. Мы начнем с одной из самых элементарных проблем: деление на ноль.
Деление по модулю в практике Python или как использовать оператор %
Python поддерживает широкий спектр арифметических операторов, которые вы можете использовать при работе с числами в вашем коде. Одним из этих операторов является оператор деления по модулю ( % ), который возвращает остаток от деления двух чисел.
В этом уроке вы узнаете:
Об операторе деления по модуля иногда забывают. Но хорошее понимание этого оператора даст вам бесценный инструмент в своём арсенале инструментов Python.
В этом уроке:
Деление по модулю в математике ↑
Классический пример модульной арифметики — двенадцать часов. Двенадцатичасовые часы имеют фиксированный набор значений от 1 до 12. При подсчете двенадцатичасовых часов вы считаете до модуля 12, а затем возвращаетесь к 1. Двенадцатичасовые часы можно классифицировать как «modulo 12», иногда сокращается до «mod 12».
Оператор деление по модулю используется, когда вы хотите сравнить число с модулем и получить эквивалентное число, ограниченное диапазоном модуля.
Если подумать, 17 и 5 эквивалентны в контексте mod 12. Если бы вы посмотрели на часовую стрелку в 5:00 и 17:00, она была бы в том же положении. В модульной арифметике есть уравнение, описывающее эту взаимосвязь:
Это уравнение гласит: «a и b равны по модулю n». Это означает, что a и b эквивалентны по модулю n, поскольку они имеют одинаковый остаток при делении на n. В приведенном выше уравнении n — это модуль как для a, так и для b. Используя значения 17 и 5 из предыдущих, уравнение будет выглядеть так:
Это гласит: «17 и 5 равны по модулю 12». 17 и 5 имеют одинаковый остаток 5 при делении на 12. Таким образом, в модуле 12 числа 17 и 5 эквивалентны.
Подтвердить это можно с помощью деления:
Обе операции имеют одинаковый остаток 5, поэтому они эквивалентны по модулю 12.
Основы работы с операторами деления модуля Python ↑
Оператор деления по модулю, как и другие арифметические операторы, может использоваться с числовыми типами int и float. Как вы увидите позже, его также можно использовать с другими типами, такими как math.fmod(), decimal.Decimal и вашими собственными классами.
Оператор деления по модулю с int ↑
В большинстве случаев вы будете использовать оператор деления по модулю с целыми числами. Оператор деления по модулю, когда он используется с двумя положительными целыми числами, вернет остаток от стандартного евклидова деления или деление с остатком એ :
Будь осторожен! Как и в случае с оператором деления ( / ), Python вернет ошибку ZeroDivisionError, если вы попытаетесь использовать оператор по модулю с делителем 0:
Далее вы узнаете, как использовать оператор деления по модулю чисел с плавающей точкой.
Оператор деления по модулю чисел плавающей точкой (float) ↑
Альтернативой использованию числа с плавающей запятой с оператором по модулю является использование math.fmod() для выполнения операций по модулю над значениями с плавающей запятой:
В следующем разделе вы более подробно исследуете использование оператора по модулю с отрицательными операндами.
Как и другие арифметические операторы, оператор по модулю и math.fmod() могут столкнуться с проблемами округления и точности при работе с арифметикой с плавающей запятой:
Если для вашего приложения важно поддерживать точность с плавающей запятой, вы можете использовать оператор по модулю с decimal.Decimal. Вы рассмотрите это позже.
Оператор деления по модулю с отрицательным операндом ↑
Все операции деления по модулю, которые вы видели до этого момента, использовали два положительных операнда и возвращали предсказуемые результаты. Когда вводится отрицательный операнд, все становится сложнее.
Как выясняется из, способ, которым компьютеры определяют результат операции деления по модулю с отрицательным операндом, оставляет неоднозначность относительно того, должен ли остаток принимать знак делимого (число, которое делится) или знак делителя (число, на которое делится делимое). Разные языки программирования обрабатывают это по-разному.
Например, в JavaScript остаток примет знак делимого:
Остаток в этом примере, 2, положительный, поскольку он принимает знак делимого, 8. В Python и других языках вместо этого остаток принимает знак делителя:
Это уравнение состоит из трех переменных:
Здесь вы можете увидеть, как такой язык, как JavaScript, получает остаток 2. Python и другие языки, в которых остаток принимает знак делителя, используют следующее уравнение:
floor() в этом уравнении означает, что он использует разделение этажей. При положительных числах деление этажа вернет тот же результат, что и усеченное деление. Но с отрицательным числом деление по этажам округляет результат в меньшую сторону, в сторону от нуля:
Оператор деления по модулю и divmod() ↑
Python имеет встроенную функцию divmod(), которая внутренне использует оператор по модулю. divmod() принимает два параметра и возвращает кортеж, содержащий результаты деления этажа и по модулю с использованием предоставленных параметров.
Ниже приведен пример использования divmod() с 37 и 5:
Вы можете видеть, что divmod(37, 5) возвращает кортеж (7, 2). 7 — это результат деления полов на 37 и 5. 2 — результат 37 по модулю 5.
Теперь, когда у вас была возможность увидеть оператор деления по модулю, используемый в нескольких сценариях, важно взглянуть на то, как Python определяет приоритет оператора деления по модулю при использовании с другими арифметическими операторами.
Приоритет оператора деления по модулю ↑
Как и другие операторы Python, для оператора деления по модулю существуют определенные правила, которые определяют его приоритет при оценке выражений. Оператор деления по модулю ( % ) имеет тот же уровень приоритета, что и операторы умножения ( * ), деления ( / ) и деления пола ( // ).
Взгляните на пример приоритета оператора деления по модулю ниже:
Операторы умножения и по модулю имеют одинаковый уровень приоритета, поэтому Python будет оценивать их слева направо. Вот шаги для вышеуказанной операции:
Если вы хотите переопределить приоритет других операторов, вы можете заключить в круглые скобки операцию, которую вы хотите выполнить в первую очередь:
В этом примере сначала вычисляется (12 – 9), затем 4 * 10 и, наконец, 40 % 3, что равно 1.
Оператор деления по модулю Python на практике ↑
Теперь, когда вы ознакомились с основами оператора Python деления по модулю, вы рассмотрите несколько примеров его использования для решения реальных задач программирования. Иногда бывает сложно определить, когда использовать в коде оператор деления по модулю. Приведенные ниже примеры дадут вам представление о многих способах его использования.
Как проверить, четное или нечетное число ↑
В этом разделе вы увидите, как с помощью оператора по модулю определить, четное или нечетное число. Используя оператор по модулю с модулем 2, вы можете проверить любое число, чтобы узнать, делится ли оно без остатка на 2. Если оно делится без остатка, то это четное число.
Здесь num % 2 будет равно 0, если num четное, и 1, если num нечетное. Проверка против 0 вернет логическое значение True или False в зависимости от того, является ли число четным или нет.
Проверка на нечетные числа очень похожа. Чтобы проверить нечетное число, вы инвертируете проверку равенства:
Ответ на этот вопрос — да и нет. Технически эта функция будет работать так же, как Python вычисляет по модулю с целыми числами. Тем не менее, вам следует избегать сравнения результата операции деления по модулю с 1, поскольку не все операции деления по модулю в Python будут возвращать один и тот же остаток.
Вы можете понять, почему, в следующих примерах:
Если вы будете сравнивать операцию Python по модулю с 0, у вас не должно возникнуть проблем с проверкой четных и нечетных чисел или любых других кратных чисел в вашем коде.
В следующем разделе вы узнаете, как можно использовать оператор по модулю с циклами для управления потоком вашей программы.
Как запускать код с определенными интервалами в цикле ↑
С помощью оператора Python деления по модулю вы можете запускать код через определенные промежутки времени внутри цикла. Это делается путем выполнения операции деления по модулю с текущим индексом цикла и модулем. Номер модуля определяет, как часто код, зависящий от интервала, будет выполняться в цикле.
Прежде чем разбирать функцию более подробно, взгляните на нее в действии:
Как видите, список имен разделен на три строки, максимум по три имени в каждой строке. по умолчанию модуль равен 3, но вы можете указать любое число:
Не вдаваясь в подробности, синтаксис: — ^ 15 предписывает print () выполнять следующие действия:
Теперь, когда имя напечатано в строке, взгляните на основную часть split_names_into_rows() :
Этот код берет текущий индекс итерации и, используя оператор по модулю, сравнивает его с модулем. Если результат равен 0, то он может запускать код, зависящий от интервала. В этом случае функция вызывает print() для добавления новой строки, которая начинает новую строку.
Приведенный выше код — это только один пример. Использование шаблона index % modulus == 0 позволяет запускать другой код через определенные промежутки времени в ваших циклах. В следующем разделе вы немного углубитесь в эту концепцию и рассмотрите циклическую итерацию.
Как создать циклическую итерацию ↑
Циклическая итерация описывает тип итерации, которая сбрасывается при достижении определенной точки. Как правило, этот тип итерации используется для ограничения индекса итерации определенным диапазоном.
Вы можете использовать оператор деления по модулю для создания циклической итерации. Взгляните на пример использования библиотеки turtle для рисования формы:
В приведенном выше коде используется бесконечный цикл для рисования повторяющейся формы звезды. После каждых шести итераций он меняет цвет пера. Размер пера увеличивается с каждой итерацией, пока i не сбрасывается обратно в 0. Если вы запустите код, вы должны получить что-то похожее на это:
Важные части этого кода выделены ниже:
Вы можете увидеть шаги итерации ниже для более подробного пояснения:
Как конвертировать единицы измерения ↑
В этом разделе вы узнаете, как использовать оператор деления по модулю для преобразования единиц. В следующих примерах единицы меньшего размера преобразуются в единицы большего размера без использования десятичных знаков. Оператор деления по модулю используется для определения любого остатка, который может существовать, когда меньшая единица не делится без остатка на большую единицу.
В этом первом примере преобразуем дюймы в футы. Оператор деления по модулю используется для получения оставшихся дюймов, которые неравномерно не делятся на футы. Оператор деления без остатка ( // ) используется для округления общего количества футов в меньшую сторону:
Вот пример используемой функции:
Разбив это, вы можете увидеть, что функция выполняет следующее:
Вы можете увидеть, как это работает, ниже:
Хотя в приведенных выше примерах рассматривается только преобразование дюймов в футы и минут в дни, вы можете использовать любые типы единиц с оператором по модулю, чтобы преобразовать меньшую единицу в большую единицу.
Ниже операторы деления без остатка и по модулю были заменены на divmod() :
Как видите, divmod(total_inches, 12) возвращает кортеж, который распакован в футы и дюймы.
Если вы попробуете эту обновленную функцию, то получите те же результаты, что и раньше:
Вы получите тот же результат, но теперь код более лаконичен. Вы также можете обновить convert_minutes_to_days() :
Использование divmod() необязательно для всех ситуаций, но здесь имеет смысл, поскольку при расчетах преобразования единиц используется как деление этажа, так и модуль.
Теперь, когда вы узнали, как использовать оператор по модулю для преобразования единиц, в следующем разделе вы узнаете, как можно использовать оператор по модулю для проверки простых чисел.
Как определить, является ли число простым числом ↑
В следующем примере вы увидите, как можно использовать оператор Python по модулю, чтобы проверить, является ли число простым. Простое число — это любое число, которое содержит только два делителя: 1 и само себя. Некоторые примеры простых чисел: 2, 3, 5, 7, 23, 29, 59, 83 и 97.
Приведенный ниже код представляет собой реализацию для определения простоты числа с помощью оператора по модулю:
Прежде чем вы более внимательно посмотрите на функцию, вот результаты с использованием некоторых других чисел:
Углубившись в код, вы увидите, что он начинается с проверки, меньше ли num 2. Простые числа могут быть только больше или равны 2. Если num меньше 2, то выполнение функции не требуется. Он просто напечатает сообщение и сделает возврат:
Если num больше 2, функция проверяет, является ли num простым числом. Чтобы проверить это, функция выполняет итерацию по всем числам от 2 до квадратного корня из числа, чтобы увидеть, делятся ли они на число поровну. Если одно из чисел делится равномерно, значит, был найден множитель, и число не может быть простым числом.
Вот основная часть функции:
Здесь есть что распаковать, так что давайте рассмотрим это шаг за шагом.
Внутри цикла while оператор по модулю проверяет, делится ли num без остатка на i :
После завершения цикла while код проверяет, не были ли найдены какие-либо дополнительные факторы:
Если в списке factors существует более одного кортежа, то num не может быть простым числом. Для непростых чисел коэффициенты распечатываются. Для простых чисел функция печатает сообщение о том, что num является простым числом.
Как реализовать шифрование ↑
Оператор деления по модулю в Python может использоваться для создания шифров. Шифр એ — это тип алгоритма для выполнения шифрования и дешифрования входных данных, обычно текста. В этом разделе вы познакомитесь с двумя шифрами: шифр Цезаря и шифр Виженера.
Шифр Цезаря
Шифр Цезаря работает, взяв зашифровываемую букву и сдвинув ее на определенное количество позиций влево или вправо в алфавите. Какая бы буква ни была в этой позиции, используется как зашифрованный символ. Это же значение сдвига применяется ко всем символам в строке.
Например, если смена была 5, затем A сдвинется на пять букв вверх, чтобы стать F, B станет G и так далее. Ниже вы можете увидеть процесс шифрования текста REALPYTHON со сдвигом 5:
В результате получается шифр WJFQUDYMTS.
Расшифровка шифра выполняется изменением сдвига в обратном направлении. Процессы шифрования и дешифрования можно описать следующими выражениями, где char_index — это индекс символа в алфавите:
Этот шифр использует оператор по модулю, чтобы гарантировать, что при сдвиге буквы индекс будет перебираться, если будет достигнут конец алфавита. Теперь, когда вы знаете, как работает этот шифр, взгляните на его реализацию:
decrypt включена, так что одна функция может использоваться для обработки как шифрования, так и дешифрования. Эта реализация может обрабатывать только буквенные символы, поэтому функция сначала проверяет, является ли текст буквенным символом в кодировке ASCII:
Затем функция определяет три переменные для хранения символов ASCII нижнего регистра, символов ASCII верхнего регистра и результатов шифрования или дешифрования:
Наконец, caesar_cipher() перебирает отдельные символы в тексте и выполняет следующие действия для каждого символа:
После завершения цикла перебора текстового значения возвращается результат:
Вот еще раз полный код:
Теперь запустите код в Python REPL, используя текст meetMeAtOurHideOutAtTwo со сдвигом 10 :
С шифром Цезаря интересно поиграть, чтобы познакомиться с криптографией. Хотя шифр Цезаря редко используется сам по себе, он является основой для более сложных подстановочных шифров. В следующем разделе вы познакомитесь с одним из потомков шифра Цезаря, шифром Виженера.
Шифр Виженера
Шифр Виженера એ — это полиалфавитный шифр подстановки. Для шифрования он использует разные шифры Цезаря для каждой буквы входящего текста. Шифр Виженера использует ключевое слово, чтобы определить, какой шифр Цезаря следует использовать для поиска буквы шифра.
Вы можете увидеть пример процесса шифрования на следующем изображении. В этом примере вводимый текст REALPYTHON зашифрован с использованием ключевого слова MODULO:
Для каждой буквы входящего текста REALPYTHON используется буква ключевого слова MODULO, чтобы определить, какой столбец шифра Цезаря следует выбрать. Если ключевое слово короче вводимого текста, как в случае с MODULO, то буквы ключевого слова повторяются до тех пор, пока все буквы вводимого текста не будут зашифрованы.
Ниже представлена реализация шифра Виженера. Как вы увидите, оператор деления по модулю используется в функции дважды:
Вы могли заметить, что подпись для vigenere_cipher() очень похожа на caesar_cipher() из предыдущего раздела:
В приведенном выше коде вы можете увидеть, как функция впервые использует оператор деления по модулю:
Для каждой буквы входящего текста несколько шагов определяют, как ее зашифровать или расшифровать:
Взгляните на эти шаги в приведенном ниже коде:
Вы можете видеть, что индексы для расшифровки и шифрования рассчитываются по-разному. Поэтому в этой функции используется расшифровка. Таким образом, вы можете использовать эту функцию как для шифрования, так и для дешифрования.
После определения индекса вы обнаружите, что функция использует оператор по модулю во второй раз:
index % 26 гарантирует, что индекс символа не превышает 25, таким образом гарантируя, что он остается внутри алфавита. С помощью этого индекса зашифрованный или дешифрованный символ выбирается из верхнего регистра и добавляется к результатам.
Вот еще раз полный код шифра Виженера:
Теперь запустите его в Python REPL:
Хорошо! Теперь у вас есть рабочий шифр Виженера для шифрования текстовых строк.
Расширенные возможности оператора деления по модулю Python ↑
Использование оператора деления по модулю Python с decimal.Decimal ↑
Вот несколько примеров использования целых чисел с decimal.Decimal и оператором по модулю:
Вот некоторые числа с плавающей запятой, используемые с decimal.Decimal и оператором деления по модулю:
Как видно из приведенных выше примеров, работа с decimal.Decimal и оператором деления по модулю аналогична работе с другими числовыми типами. Вам просто нужно иметь в виду, как он определяет знак результата при работе с отрицательным операндом.
В следующем разделе вы увидите, как можно переопределить оператор по модулю в своих классах, чтобы настроить его поведение.
Использование оператора деления по модулю Python с настраиваемыми классами ↑
Сейчас, если вы помните из приведенного выше раздела о преобразовании единиц, convert_minutes_to_day() использовал оператор Python деления по модулю для преобразования total_mins в дни, часы и минуты. Теперь вы реализуете модифицированную версию этого метода, чтобы увидеть, как можно использовать свой собственный класс с оператором деления по модулю:
Если вы загрузите этот модуль в Python REPL, вы можете использовать его следующим образом:
Вот полный код после изменений:
Теперь, вызвав код в Python REPL, вы увидите, что он намного лаконичнее:
Заключение ↑
На первый взгляд, оператор деления по модулю Python может не привлечь вашего внимание. Тем не менее, как вы видели, в этом скромном операторе есть так много всего. Вы увидели множество различных применений оператора деления по модулю, от проверки чётности чисел до шифрования текста.
В этом уроке вы узнали, как:
Благодаря знаниям, полученным в этом уроке, теперь вы сможете с большим успехом начать использовать оператор деления по модулю в своем собственном коде. Удачного питонинга!
Опубликовано Вадим В. Костерин
ст. преп. кафедры ЦЭиИТ. Автор более 130 научных и учебно-методических работ. Лауреат ВДНХ (серебряная медаль). Посмотреть больше записей