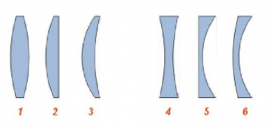
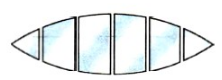
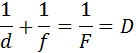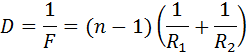Линзу у которой края тоньше чем середина называют

Линза. Виды линз. Фокусное расстояние.

теория по физике 🧲 оптика

Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.

Линза — прозрачное тело, ограниченное сферическими поверхностями.

Какими бывают линзы?

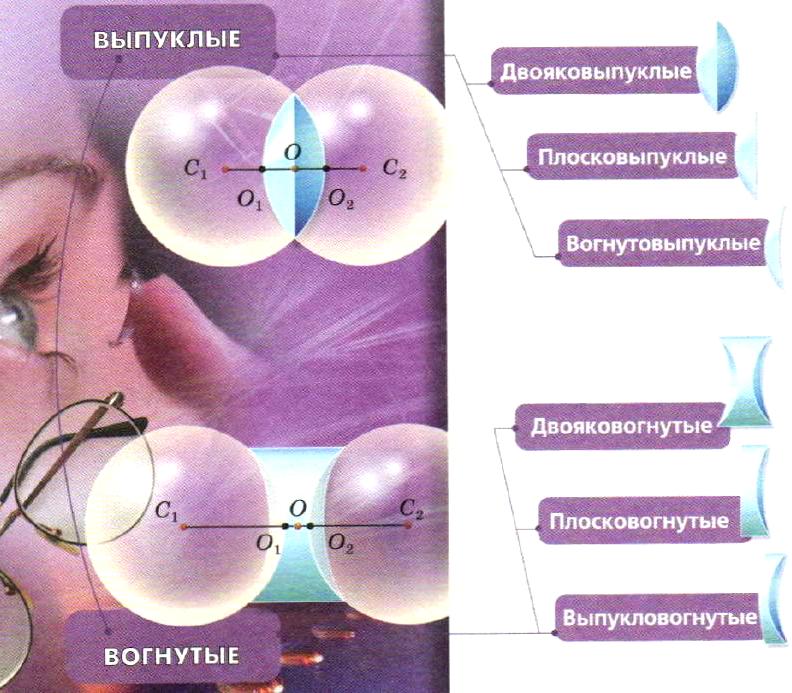
По форме различают следующие виды линз:

Выпуклые линзы тоже имеют разновидности:

Разновидности вогнутых линз:

Тонкая линза

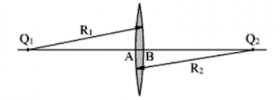
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R₁ и R₂. Такие линзы называют тонкими.

Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.

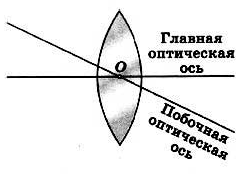
Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O₁O₂).

Оптический центр линзы — точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.

Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.

Изображение в линзе

Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.

Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.

Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.

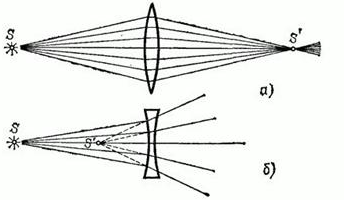
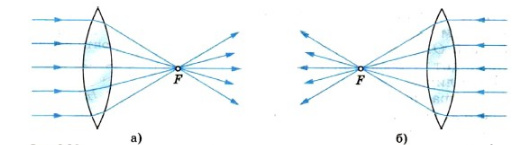
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.

Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.

Собирающая линза

Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.

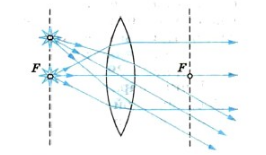
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.

Главный фокус линзы обозначают буквой F.

Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).

В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.

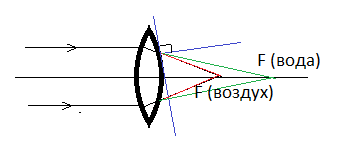
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?

Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.

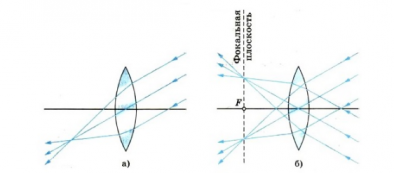
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.

Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.

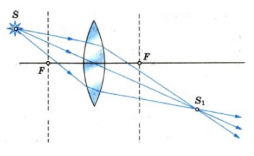
Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.

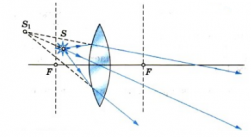
Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.

Рассеивающая линза

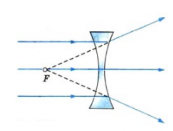
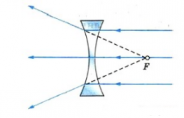
Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.

Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.

Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.

Оптическая сила линзы

Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.

Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.

Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:

На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу. Какова приблизительно оптическая сила этой линзы?

Источник

Частная школа. 9 класс

Конспекты, контрольные, тесты

Линзы

Конспект по физике для 9 класса «Линзы». Что такое линзы. Что такое оптическая ось и оптический центр линзы. Что такое оптическая сила линзы и какова её единица.

Линзы.

Зная законы отражения и преломления света, можно решать разнообразные задачи, связанные с управлением световыми пучками. Одними из старейших оптических устройств, используемых для этого, являются линзы. Линзы являются составной частью фотоаппаратов, микроскопов, телескопов и т. д. Хорошо всем знакомые очки, служащие для коррекции зрения, состоят из оправы и линз. Широкое распространение в последнее время получили контактные линзы, использующиеся для коррекции близорукости и дальнозоркости.

ВИДЫ ЛИНЗ

Линзой (от лат. lens — чечевица) называют прозрачное тело, ограниченное с двух сторон сферическими поверхностями. Линзы бывают двух видов: выпуклые и вогнутые. Линзу, у которой края тоньше, чем середина, называют выпуклой. Линзу, у которой края толще, чем середина, называют вогнутой.

Линзы использовались ещё в Древней Греции и в Римской империи для добывания огня с помощью солнечного света. К концу XIII в. относят первые документальные свидетельства появления очков. До XVI в. пользовались очками только с выпуклыми линзами.

ХАРАКТЕРИСТИКИ ЛИНЗ

Прямую, проходящую через центры С₁ и С₂ сферических поверхностей, ограничивающих линзу, называют главной оптической осью линзы.

Мы будем рассматривать линзы, толщина которых мала по сравнению с радиусами поверхностей. Такие линзы называют тонкими. Для этих линз вершины сферических поверхностей (точки О₁ и О₂) практически совпадают. Эту точку называют оптическим центром линзы (точка О).

Направим на выпуклую линзу пучок лучей, параллельный главной оптической оси. После преломления в линзе эти лучи пересекутся в одной точке F, которая находится на главной оптической оси. Эту точку называют фокусом линзы. Если световой пучок пропустить через линзу с другой стороны, то будет наблюдаться та же картина. У каждой линзы два фокуса — по одному с каждой стороны.

Расстояние от линзы до её фокуса называют фокусным расстоянием линзы и обозначают F.

Прохождение светового пучка сквозь линзу можно наблюдать на простом опыте. На пути светового пучка устанавливается линза, а за линзой помещается передвижной экран. Последовательно перемещая экран, можно наблюдать за изменением размера и яркости светового пятна. В том положении экрана, в котором мы видим маленькое яркое пятно, находится фокус линзы.

СОБИРАЮЩИЕ И РАССЕИВАЮЩИЕ ЛИНЗЫ

В зависимости от того, что происходит после преломления с пучком световых лучей, параллельных главной оптической оси линзы, линзы делят на собирающие и рассеивающие.

Пучок лучей, направленный на выпуклую линзу параллельно её главной оптической оси, после преломления соберётся в одной точке — фокусе линзы. Поэтому выпуклую линзу называют собирающей.

Если же такой пучок лучей направить на вогнутую линзу, то после преломления в линзе пучок станет расходящимся.

Если продолжить преломлённые лучи в обратном направлении, то они сойдутся в одной точке с той стороны линзы, с какой падает на неё свет. Эту точку называют мнимым фокусом, а саму вогнутую линзу — рассеивающей.

Фокусное расстояние линзы зависит от степени кривизны её поверхностей. Линза с более выпуклыми поверхностями преломляет лучи сильнее, чем линза с менее выпуклыми поверхностями. Поэтому её фокусное расстояние меньше: F₁

Вы смотрели Конспект по физике для 9 класса «Линзы».

Источник

Линзы

Линзы

Линзой называется прозрачное тело, ограниченное двумя криволинейными (чаще всего сферическими) или криволинейной и плоской поверхностями. Линзы делятся на выпуклые и вогнутые.

Линзы, у которых середина толще, чем края, называются выпуклыми. Линзы, у которых середина тоньше, чем края, называются вогнутыми.

Если показатель преломления линзы больше, чем показатель преломления окружающей среды, то в выпуклой линзе параллельный пучок лучей после преломления преобразуется в сходящий пучок. Такие линзы называются собирающими (рис. 89, а). Если в линзе параллельный пучок преобразуется в расходящийся пучок, то эти линзы называются рассеивающими (рис. 89, б). Вогнутые линзы, у которых внешней средой служит воздух, являются рассеивающими.

Если на собирающую линзу падает пучок лучей, параллельных главной оптической оси, то после преломления в линзе они собираются в одной точке F, которая называется главным фокусом линзы (рис. 90, а).

Плоскость, проходящая через главный фокус линзы перпендикулярно к главной оптической оси, называется фокальной (рис. 91). Пучок лучей, падающих на линзу параллельно какой-либо побочной оптической оси, собирается в точке пересечения этой оси с фокальной плоскостью.

Построение изображения точки и предмета в собирающей линзе.

Для построения изображения в линзе достаточно взять по два луча от каждой точки предмета и найти их точку пересечения после преломления в линзе. Удобно пользоваться лучами, ход которых после преломления в линзе известен. Так, луч, падающий на линзу параллельно главной оптической оси, после преломления в линзе проходит через главный фокус; луч, проходящий через оптический центр линзы, не преломляется; луч, проходящий через главный фокус линзы, после преломления идет параллельно главной оптической оси; луч, падающий на линзу параллельно побочной оптической оси, после преломления в линзе проходит через точку пересечения оси с фокальной плоскостью.

Пусть светящаяся точка S лежит на главной оптической оси.

Рассмотрим построение изображения предмета в выпуклой линзе.

Пусть точка лежит вне главной оптической оси, тогда изображение S` можно построить с помощью любых двух лучей, приведенных на рис. 93.

Если предмет расположен в бесконечности, то лучи пересекутся в фокусе (рис. 94).

Если предмет расположен за точкой двойного фокуса, то изображение получится действительным, обратным, уменьшенным (фотоаппарат, глаз) (рис. 95).

Если предмет расположен в точке двойного фокуса, то изображение получится действительным, обратным, равным предмету (рис. 96).

Если предмет расположен между фокусом и точкой двойного фокуса, то изображение получится действительным, обратным, увеличенным (фотоувеличитель, киноаппарат, фильмоскоп) (рис. 97).

Если предмет расположен в фокусе, то изображение будет в бесконечности (изображения не будет) (рис. 98).

Если предмет расположен между фокусом и оптическим центром линзы, то изображение будет мнимым, прямым, увеличенным (лупа) (рис. 99).

При любом расстоянии от предмета до рассеивающей линзы она дает мнимое, прямое, уменьшенное изображение (рис. 100).

Источник

Тонкие линзы

Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.

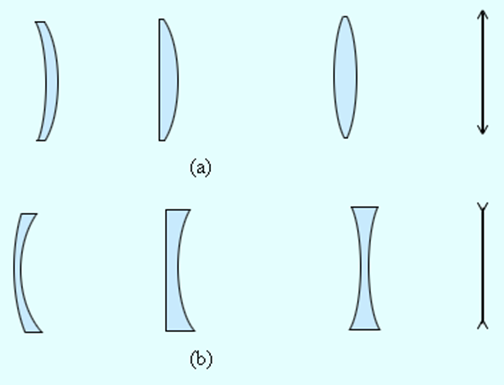
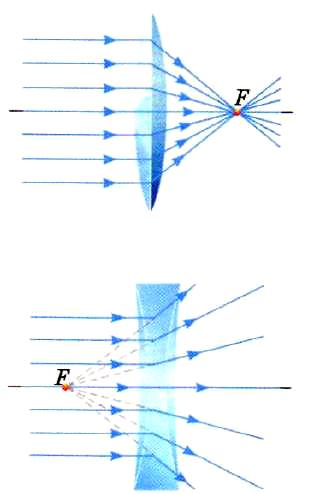
Линзы входят в состав практически всех оптических приборов. Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше (рис. 3.3.1).

Собирающие (a) и рассеивающие (b) линзы и их условные обозначения

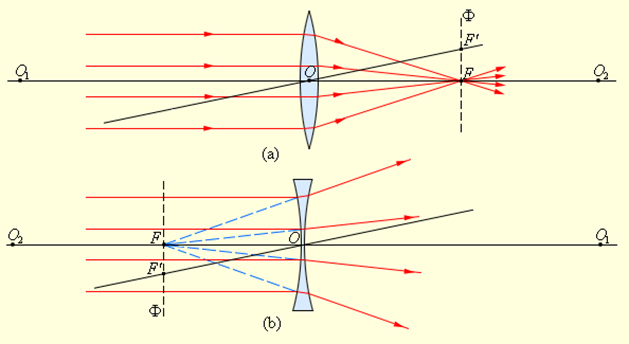
Прямая, проходящая через центры кривизны O₁ и O₂ сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз приближенно можно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы O. Луч света проходит через оптический центр линзы, не отклоняясь от первоначального направления. Все прямые, проходящие через оптический центр, называются побочными оптическими осями.

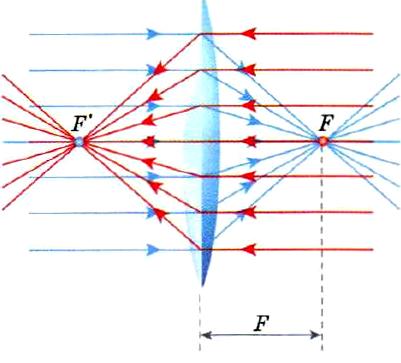
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, расположенных симметрично на главной оптической оси относительно линзы. У собирающих линз фокусы действительные, у рассеивающих – мнимые. Пучки лучей, параллельных одной из побочных оптических осей, после прохождения через линзу также фокусируются в точку F’, которая расположена при пересечении побочной оси с фокальной плоскостью Ф, то есть плоскостью, перпендикулярной главной оптической оси и проходящей через главный фокус (рис. 3.3.2). Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначается той же буквой F.

Преломление параллельного пучка лучей в собирающей (a) и рассеивающей (b) линзах. Точки O₁ и O₂ – центры сферических поверхностей, O₁O₂ – главная оптическая ось, O – оптический центр, F – главный фокус, F’ – побочный фокус, OF’ – побочная оптическая ось, Ф – фокальная плоскость

Основное свойство линз – способность давать изображения предметов. Изображения бывают прямыми и перевернутыми, действительными и мнимыми, увеличенными и уменьшенными.

Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей. Примеры таких построений представлены на рис. 3.3.3 и 3.3.4.

Построение изображения в собирающей линзе

Построение изображения в рассеивающей линзе

Следует обратить внимание на то, что некоторые из стандартных лучей, использованных на рис. 3.3.3 и 3.3.4 для построения изображений, не проходят через линзу. Эти лучи реально не участвуют в образовании изображения, но они могут быть использованы для построений.

Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:

Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м:

Формула тонкой линзы аналогична формуле сферического зеркала. Ее можно получить для параксиальных лучей из подобия треугольников на рис. 3.3.3 или 3.3.4.

Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений;

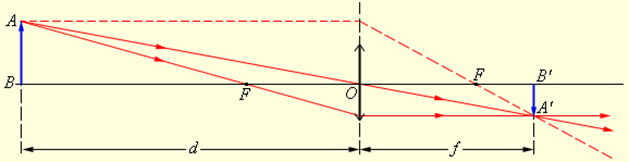
d 0 (линза собирающая), d = 3F > 0 (действительный предмет).

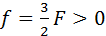
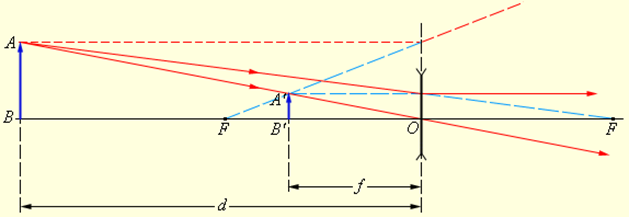
По формуле тонкой линзы получим: , следовательно, изображение действительное.

В случае, изображенном на рис. 3.3.4, F 0 (действительный предмет), 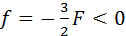, то есть изображение мнимое.

В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения h’ и предмета h. Величине h’, как и в случае сферического зеркала, удобно приписывать знаки плюс или минус в зависимости от того, является изображение прямым или перевернутым. Величина h всегда считается положительной. 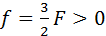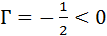Поэтому для прямых изображений Γ > 0, для перевернутых Γ 0, , следовательно, – изображение перевернутое и уменьшенное в 2 раза.

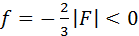
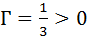
В примере с рассеивающей линзой (рис. 3.3.4): d = 2|F| > 0, ; следовательно, – изображение прямое и уменьшенное в 3 раза.

Оптическая сила D линзы зависит как от радиусов кривизны R₁ и R₂ ее сферических поверхностей, так и от показателя преломления n материала, из которого изготовлена линза. В курсах оптики доказывается следующая формула:

Радиус кривизны выпуклой поверхности считается положительным, вогнутой – отрицательным. Эта формула используется при изготовлении линз с заданной оптической силой.

Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета. Это второе изображение также может быть действительным или мнимым. Расчет оптической системы из двух тонких линз сводится к двукратному применению формулы линзы, при этом расстояние d₂ от первого изображения до второй линзы следует положить равным величине l – f₁, где l – расстояние между линзами. Рассчитанная по формуле линзы величина f₂ определяет положение второго изображения и его характер (f₂ > 0 – действительное изображение, f₂ Опубликовано в разделах: Оптика, Геометрическая оптика

Источник