Лобачевский доказал что параллельные прямые пересекаются
Новое в блогах
Пересекаются ли параллельные или Что говорил Лобачевский?
Недавно в посте на околонаучные темы один из комментаторов завел разговор о геометрии Лобачевского (что он ее не понимает) и даже вроде попросил объяснить. Я тогда ограничилась утверждением, что понимаю. Объяснять эту теорию в ограниченных рамках комментария и одним текстом (без рисунков) показалось мне невозможным.
Однако, подумав, я все же решила попробовать дать небольшой популярный экскурс в эту теорию.
Немного предыстории. Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких постулатов (аксиом). Считалось, что эти аксиомы «очевидны», т.е. отражают свойства реального (физического) пространства.
Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова:
«Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну-то прямую можно провести, является не аксиомой, а теоремой.
При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая – одна!
Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он, как это часто делается в математике, выбрал метод «от противного», т.е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится! Т.е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование!
Конечно, в первое время его выкладки не признавали, смеялись над ним. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что ЧИСТО ЛОГИЧЕСКИ теория Лобачевского ничем не хуже евклидовой.
Один из остроумных способов убедиться в этом – придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один.
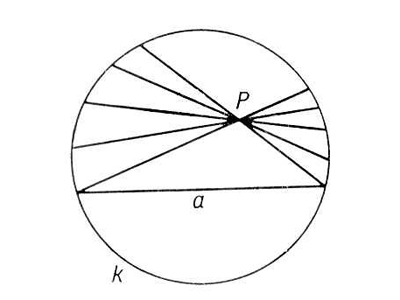
Пожалуй, самой простой является модель Пуанкаре. Вы можете сами построить ее нехитрыми приборами.
Начертите не листке бумаги прямую. Возьмите циркуль и, ставя его иглу на эту прямую, нарисуйте полуокружности, находящиеся с одной стороны от прямой. Теперь сотрите прямую (и с ней – концевые точки полуокружностей). Так вот, эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского!
Действительно, выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли) Т.е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их – бесконечное количество.
Можно заметить, что треугольники в этой модели не такие, как на плоскости (евклидовой): сумма их углов меньше 180 градусов! Впрочем, чем меньше треугольник, тем больше сумма его углов. В «малом», на небольших расстояниях, геометрия Лобачевского практически совпадает с геометрией Евклида. Поэтому, вообще говоря, мы не сможем «экспериментально» отличить одну от другой, если окажется, что доступные нам (космические) расстояния– малы для этой цели.
Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства. Математики поняли, что все, что они могут сказать: если верны такие-то аксиомы, то верны и такие-то теоремы. Ну, а что такое «множества», «точки», «прямые», «углы», «расстояния», и т.п. – этого мы не знаем! Прямо как у Станислава Лема: «Сепульки – это объекты для сепулькирования»
«Говорят, Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чем говорим, и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. [ … ] Таким образом, одна из главных функций математического доказательства – создание надежной основы для проникновения в суть вещей.»
Геометрия Лобачевского
Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.
Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.
И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.
Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.
Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.
Аксиома параллельности Лобачевского выглядит следующим образом:
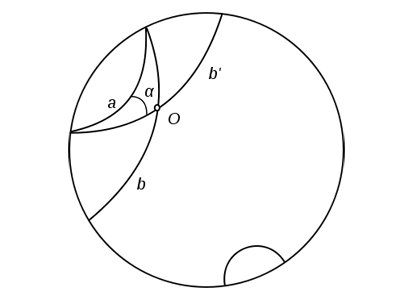
Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.
Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.
Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.
Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.
В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».
Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».
Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:
В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.
Пять мифов о геометрии Лобачевского
Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой.
На самом деле геометрия Лобачевского не слишком сильно отличается от привычной нам Евклидовой. Дело в том, что из пяти постулатов Евклида четыре первых Лобачевский оставил без изменения. То есть он согласен с Евклидом в том, что между двумя любыми точками можно провести прямую, что ее всегда можно продолжить до бесконечности, что из любого центра можно провести окружность с любым радиусом, и что все прямые углы равны между собой. Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.
Миф второй. В теории Лобачевского параллельные прямые пересекаются
Это не так. На самом деле пятый постулат Лобачевского звучит так: «На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную». Иными словами, для одной прямой можно провести как минимум две прямые через одну точку, которые не будут ее пересекать. То есть в этом постулате Лобачевского речи о параллельных прямых вообще не идет! Говорится лишь о существовании нескольких непересекающихся прямых на одной плоскости. Таким образом, предположение о пересечении параллельных прямых родилось из-за банального незнания сути теории великого российского математика.
Миф четвертый. Геометрия Лобачевского не применима в реальной жизни
Миф пятый. Лобачевский первым создал неевклидову геометрию
Это не совсем так. Параллельно с ним и независимо от него к подобным выводам пришли венгерский математик Янош Бойяи и знаменитый немецкий ученый Карл Фридрих Гаусс. Однако труды Яноша не были замечены широкой публикой, а Карл Гаусс и вовсе предпочел не издаваться. Поэтому именно наш ученый считается первопроходцем в этой теории. Однако существует несколько парадоксальная точка зрения, что первым неевклидову геометрию придумал сам Евклид. Дело в том, что он самокритично считал свой пятый постулат не очевидным, поэтому большую часть из своих теорем он доказал, не прибегая к нему.
А «параллельные» прямые пересекаются в проективной геометрии
Наверняка вы когда–нибудь слышали, что в геометрии Лобачевского параллельные прямые пересекаются. Конечно же, это не так. И даже наоборот.
Из школьного курса геометрии мы знаем, что [далее менторским тоном] «через точку, не лежащую на прямой, можно провести прямую, параллельную данной, и только одну».
Это утверждение – наиболее популярное перефразирование пятого постулата Евклида, который в своё время подложил здоровенную свинью своим последователям. Дело в том, что в его «Началах» первые четыре постулата сформулированы очень просто и очевидно. Вот они:
В пятом же постулате Евклид решил потроллить математиков, и вместо того, чтобы написать что–нибудь столь же простое, например, «Прямоугольники существуют» (и баста!), он начал запутывать: «Если прямая, пересекающая две прямые, образует внутренние односторонние углы… бла–бла–бла…»
И все подумали: что–то он здесь темнит, не может быть аксиома такой сложной. Не распознав подвох, математики в течение 2 тысяч лет пытались избавиться от этого постулата и доказать его через другие постулаты и аксиомы. Сначала древние греки, потом арабы, потом европейцы. И каждый думал, что он успешно доказал этот постулат, но потом выяснялось, что его доказательство базируется на каком–нибудь очевидном, но не доказанном утверждении, равнозначном самому постулату. Таких утверждений набралось огромное множество. Вот ещё некоторые из них:
Последний пункт и играет ключевую роль в путанице с геометрией Лобачевского. Но об этом чуть позже.
Наконец, наиболее продвинутые из математиков стали пытаться применить доказательство от противного[Евклида] – то есть, предположить, что пятый постулат не верен, и вывести из этого какое–нибудь противоречие. Первым был итальянец Саккери (первая половина XVIII в.), который очень досадовал, что никак не может найти это противоречие. В конце концов, он сделал ошибку в вычислениях, получил противоречие и радостно вздохнул.
Мало–помалу математики стали что–то подозревать. И уже начались попытки отказаться от пятого постулата не в целях найти противоречие, а просто посмотреть, что же получится. Первых успехов добился Ламберт, который во второй половине XVIII в. построил непротиворечивую геометрию на сфере, в которой сумма углов треугольника всегда больше 180° и все прямые пересекаются. Однако в сферической геометрии нарушается не только пятый постулат, но и как минимум первые три. Кстати, четвёртый всё–таки был доказан и исключен из постулатов.
Ламберт также исследовал геометрию, в которой сумма углов треугольника всегда меньше 180°, не нашёл в ней противоречий, но не смог представить себе этакую мнимую сферу. Поэтому он не стал развивать тему, ограничившись заявлением, что доказать пятый постулат невозможно.
Дальше над этим работали Швейкарт и Гаусс. Гаусс отлично всё понимал, но понимал также и то, что втирать подобное почтенному научному сообществу – себе дороже. Заминусуют, потом вообще ничего не сможешь постить. Поэтому они оба тихо молчали себе в трубочку.
Первым, кто во всеуслышание заявил о неевклидовой геометрии, был Лобачевский. Сначала в докладе в 1826 году, затем в публикации 1829 года. Естественно на него посыпались все шишки, и он чуть было не лишился поста ректора Казанского университета. Он был не понят и осмеян, как в России, так и за рубежом. Но продолжал настаивать и отстаивать, и продвинулся в исследовании новой геометрии дальше всех. И с тех пор она носит его имя.
Почти как в песне поётся:
One deserves the credit, one deserves the blame
And Nikolai Ivanovich Lobachevsky is his name
Независимо от Лобачевского, но на три года позже него, публикует работу о неевклидовой геометрии венгерский математик Бойяи, которая также остаётся незамеченной.
Гаусс высоко оценивал работу Лобачевского, но только в частной переписке. Он даже пытался учить русский язык, чтобы почитать его русскоязычные публикации. В 1860–х годах (уже после смерти и Гаусса, и Лобачевского) переписка Гаусса становится достоянием общественности, и его восторженные отзывы о Лобачевском привлекают внимание к русскому учёному и его идеям. В общем, справедливость восторжествовала, но как всегда посмертно.
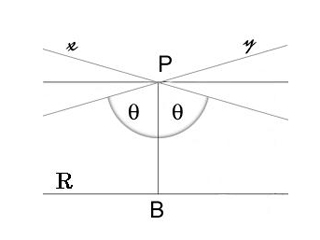
Итак, в геометрии Лобачевского через одну точку можно провести как минимум две прямые, параллельные данной, а вообще бесконечно много. Казалось бы, раз параллельные прямые проходят через одну точку, то они пересекаются. Да, они пересекаются, но фокус в том, что они не параллельны друг другу, хоть обе параллельны третьей прямой.
Ну и кроме этого, как вы, наверное, догадываетесь, сумма углов треугольника всегда меньше 180°, площадь треугольника ограничена константой, отношение длины окружности к диаметру растёт с увеличением окружности и т.д. Всё в таком духе. Да и теорема Пифагора не работает.
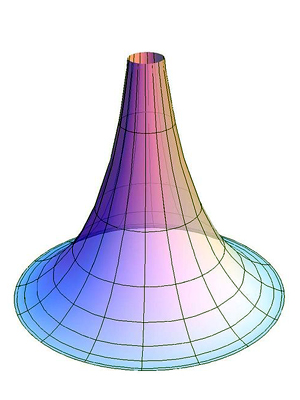
Как же представить такую поверхность, на которой работает геометрия Лобачевского? А вот она – на КДПВ, с очень сексуальным треугольничком на ней. Это так называемая гиперболическая плоскость. Если сфера – повсюду выпуклая поверхность, то гиперболическая плоскость – повсюду вогнутая, как какая–нибудь воронка или седло, только бесконечная. Как у сферы есть радиус (кривизны), так и у плоскости Лобачевского есть некий показатель кривизны. Только у сферы эта кривизна положительна, а у плоскости Лобачевского – отрицательна.
На очень маленьком масштабе, либо при увеличении показателя кривизны, геометрия Лобачевского приближается к евклидовой. Так что, вполне может оказаться, что мы живём в пространстве Лобачевского с достаточно большим показателем кривизны, поэтому не замечаем этого в наших масштабах. В частности, из теории относительности следует, что при равномерном распределении массы во вселенной, наше пространство вполне может иметь геометрию Лобачевского. Если это действительно окажется так, то Лобачевского можно назвать Эйнштейном математики.
А позавчера 228 лет со дня рождения Николая Ивановича Лобачевского. С чем вас и поздравляю!
Геометрия Лобачевского
Из Википедии — свободной энциклопедии
Геометрия Лобачевского (или гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных аксиомах, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется её отрицанием.
Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений, при наличии других аксиом) может быть сформулирована следующим образом:
На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
В геометрии Лобачевского вместо неё принимается следующая аксиома:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Аксиома Лобачевского является точным отрицанием аксиомы Евклида (при выполнении всех остальных аксиом), так как случай, когда через точку, не лежащую на данной прямой, не проходят ни одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её, исключается в силу остальных аксиом (аксиомы абсолютной геометрии). Так, например, сферическая геометрия и геометрия Римана, в которых любые две прямые пересекаются, и следовательно, не выполнена ни аксиома о параллельных Евклида, ни аксиома Лобачевского, не совместимы с абсолютной геометрией.
Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое и философское её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки в целом.