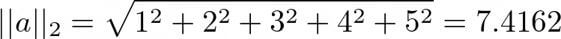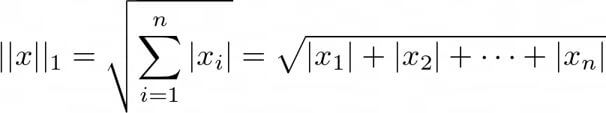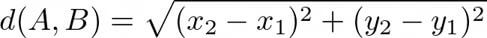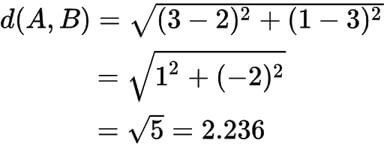np linalg norm python что делает
Норма вектора в Python – шаги для расчета
Норма вектора относится к длине или величине вектора. Существуют разные способы рассчитать длину. Норма вектора является
Норма вектора относится к длине или величине вектора. Существуют разные способы рассчитать длину. Норма вектора – неотрицательное значение. В этом руководстве мы узнаем, как рассчитать различные типы норм вектора.
Норма вектора x обозначается как: ‖ х ‖
Норма вектора – это мера ее расстояния от происхождения в векторном пространстве.
Для расчета нормы вы можете либо использовать Numpy или Scipy. Оба предлагают аналогичную функцию для расчета нормы.
В этом руководстве мы рассмотрим два типа норм, которые наиболее распространены в области машинного обучения.
Как рассчитать норму L1 вектора?
Н1 норм вектора также известен как Манхэттен Расстояние или Такси Норма Отказ Обозначение для л 1 Норма вектора x – ‖ х ‖ 1 Отказ
Чтобы рассчитать норму, вам нужно взять Сумма абсолютных векторных значений.
Давайте возьмем пример, чтобы понять это:
Для массива выше, L 1 Норма будет:
Давайте возьмем еще один пример:
Реализация Python норм L1
Посмотрим, как мы можем рассчитать l 1 Норма вектора в Python.
Использование Numpy
Код Python для расчета l 1 Норма, используя Numpy выглядит следующим образом:
Давайте попробуем вычислить его для массива с отрицательными записями в нашем примере выше.
Использование Scipy
Для расчета l 1 Использование Scipy не сильно отличается от реализации выше.
Код для такого же есть:
Код точно похоже на Numpy.
Как рассчитать норму L2 вектора?
Обозначение для L 2 Норма вектора x – ‖ х ‖ 2 Отказ
Для расчета l 2 Норма вектора, возьмите квадратный корень из суммы квадратных векторных значений.
Другое имя для л 2 Норма вектора – это Евклидово расстояние. Это часто используется для расчета ошибки в моделях машинного обучения.
Ошибка средневековой квадратной коренности является евклидое расстояние между фактическим выходом модели и ожидаемым выходом.
Целью модели обучения машины является снижение этой ошибки.
Давайте рассмотрим пример, чтобы понять это.
Л 2 Норма всегда является положительным количеством, поскольку мы докладываем значения, прежде чем добавлять их.
Реализация Python
Реализация Python выглядит следующим образом:
Здесь мы можем увидеть это по умолчанию Норма метода Возвращает L 2 норма.
Заключение
Это руководство было о расчете L 1 и л 2 Нормы в Python. Мы использовали Numpy и Scipy для расчета двух норм. Надеюсь, вы веселились с нами!
Расчет евклидова расстояния с помощью NumPy
В этом руководстве мы рассмотрим, как рассчитать евклидово расстояние между двумя точками в Python с помощью Numpy.
Что такое евклидово расстояние?
Евклидово расстояние — кратчайшая прямая между двумя точками в евклидовом пространстве.
Название происходит от Евклида, который широко известен как «отец геометрии», так как это было единственное пространство, которое люди в то время обычно задумывали. Со временем в физике и математике наблюдались различные типы пространства, такие как пространство Аффин.
В 3-мерном евклидовом пространстве кратчайшая прямая между двумя точками всегда будет прямой линией между ними.
Учитывая этот факт, евклидово расстояние не всегда является наиболее полезной метрикой для отслеживания при работе со многими размерностями, мы сосредоточимся на 2D и 3D евклидовом пространстве для расчета евклидова расстояния.
Вообще говоря, евклидова расстояние широко используется в разработке 3D-миров, а также алгоритмов машинного обучения, которые включают в себя метрики расстояния, такие как K-ближайшие соседи. Как правило, евклидово расстояние будет представлять, насколько похожи две точки данных, предполагая, что некоторая кластеризация на основе других данных уже была выполнена.
Математическая формула
Математическая формула расчета евклидова расстояния между 2 точками в 2D пространстве:
Формула легко адаптируется к 3D-пространство, а также к любому размеру:
Общая формула может быть упрощена до:
Острый глаз может заметить сходство между евклидовым расстоянием и теоремой Пифагора:
Из-за этого евклидова расстояние иногда называют расстоянием Пифагора, хотя прежнее название гораздо более известно.
Примечание: Две точки являются векторами, но выход должен быть скалярным.
Мы будем использовать NumPy для расчета этого расстояния для двух точек, и один и тот же подход используется для 2D и 3D пространств:
Расчет евклидова расстояния в Python с помощью NumPy
Во-первых, нам нужно будет установить библиотеку NumPy:
Теперь давайте импортируем его и настроим две наши точки с декартовыми координатами (0, 0, 0) и (3, 3, 3):
Вместо того, чтобы выполнять расчет вручную, мы будем использовать вспомогательные методы NumPy, чтобы сделать его еще проще!
Операции и математические функции, необходимые для расчета евклидова расстояния, довольно просты: сложение, вычитание, а также функция квадратного корня. Несколько слагаемых также можно заменить суммой:
NumPy предоставляет нам функцию np.sqrt(), представляющую функцию квадратного корня, а также функцию np.sum(), которая представляет собой сумму. При этом расчет евклидова расстояния в Python прост и интуитивно понятен:
Данная формула дает нам довольно простой результат:
Что равно 27. Осталось все, что получить квадратный корень из этого числа:
В истинном питоновом духе это можно сократить до одной строки:
Этот подход, однако, интуитивно больше похож на формулу, которую мы использовали раньше:
Это также приводит к:
np.linalg.norm()
Если бы вы установили для параметра ord какое-то другое значение p, вы бы рассчитали другие p-нормы. Например, норма L1 вектора-это расстояние Манхэттена!
Имея это в виду, мы можем использовать функцию np.linalg.norm() для легкого и гораздо более чистого вычисления евклидова расстояния, чем использование других функций:
Это приводит к печати расстояния L2/евклида:
Нормализация L2 и нормализация L1 широко используются в машинном обучении для нормализации входных данных.
Для расчета точечного произведения между 2 векторами вы можете использовать следующую формулу:
С помощью NumPy мы можем использовать функцию np.dot(), передавая два вектора.
Конечно, вы также можете сократить это до однострочного:
Использование встроенной системы math.dist()
В Python есть встроенный метод в математическом модуле, который вычисляет расстояние между 2 точками в трехмерном пространстве. Однако это работает только с Python 3.8 или более поздней версии.
math.dist()принимает два параметра, которые являются двумя точками, и возвращает евклидово расстояние между этими точками.
Примечание: Обратите внимание, что две точки должны иметь одинаковые размеры (т.е. оба в 2d или 3d пространстве).
Теперь, чтобы вычислить Евклидово расстояние между этими двумя точками, мы просто заправляем их в метод thedistdist():
Заключение
Данная метрика используется во многих контекстах в интеллектуальном анализе данных, машинном обучении и ряде других областей и является одной из фундаментальных метрик расстояния.
Основы линейной алгебры с Numpy (часть 1)
Дата публикации Sep 21, 2019
Ах, математика Вы не можете избежать этого навсегда. Вы можете попробовать, а затем попробовать больше, но рано или поздно вам понадобится некоторая базовая интуиция, если вы серьезно настроены продвинуться по карьерной лестнице в науке о данных.
Когда дело доходит до линейной алгебры, мне очень нравится эта цитата:
Если бы Data Science был Бэтменом, линейная алгебра была бы Робином. [1]
Это аккуратно отражает суть нетехническим способом.
Почему я должен изучать линейную алгебру?
Отличный вопрос
Проще говоря, если вы понимаете это, вы сможете разработать лучшую интуицию для машинного обучения и алгоритмов глубокого обучения, и вы не будете рассматривать их как черные ящики. Кроме того, вы также сможете разрабатывать алгоритмы с нуля и создавать свои собственные вариации.
Не только это, но вы также будете считаться крутым ребенком, как эти двое:
Почему я должен читать этот пост?
Этот пост, конечно, не научит вас мельчайшим деталям по этой теме, есть множество книг, которые их освещают. Пост также не будет вдаваться в доказательства, опять же, почитайте книгу какого-нибудь математического или технического факультета, если вам это нравится. Этот пост, однако, предоставит вам необходимую интуицию за линейной алгеброй (и некоторыми легкими вычислениями) в 14 различных областях.
Да, вы правильно прочитали. Я планирую охватить 14 различных тем в двух статьях. Это займет у вас некоторое время, чтобы прочитать его (и я его напишу), но если вы новичок в этом, я настоятельно рекомендую читать не более 2–3 тем в день, а затем искать в Интернете больше практических проблем.
Как устроена статья?
Итак, каждая из тем разделена на 3 части:
Теперь, когда введение закончено, давайте не будем откладывать неизбежное. Возьмите чашку кофе (или что-нибудь покрепче) и отправляйтесь со мной в удивительный мир линейной алгебры.
Вы после окончания этой статьи. ПоGIPHY
Что такое вектор?
Да, нет смысла начинать с добавления вектора, если вы понятия не имеете, что такое вектор. Для начала подумайте о векторе как о стрелке в пространстве. Вы должны иметь в виду две величины здесь:
Я имею в виду направлениекуда в космосе указывает стрелкаи величина говорит вамкак далеко вы должны идтив этом направлении. Если у вас есть только величина, но не направление, то вы говорите оскаляры, Как только вы дадите скаляру некоторое направление, он станет вектором.
Векторы чаще всего обозначаютсястрочная буква и стрелкавыше, указывая вправо:
Просто, правда?
Давайте теперь перейдем к некоторым векторным операциям, я знаю, насколько нетерпеливым вы должны быть (*смеется*).
1. Добавление вектора
Давайте погрузимся в первую векторную операцию, которая является сложением векторов (вычитание работает так же, только вы бы использовали знак минус вместо плюса, очевидно).
Об этой основной операции сказать особо нечего, только то, что она выполняетсядобавление соответствующих компонентов, Это помогает понять суть вопроса, если вы думаете о том, что происходит с вектором, а не только с точки зрения простого сложения чисел.
Посмотрите на это фото отWikipedia Commons:
Может показаться излишним, если вы услышите это в первый раз, но просто возьмите ручку и бумагу и нарисуйте это, вы сразу же поймете суть.
А вот общая формула для сложения векторов:
Сейчас я сделаю простой пример вручную, а позже реализую этот же пример на Python.
Реализация в Python:
Как видите, Numpy позволяет использовать оператор сложения, довольно аккуратно!
2. Скалярное Умножение
Позвольте мне процитировать себя из ранее в этой статье:
Если у вас есть только величина, но не направление, то вы говорите о скалярах.
Отлично, давайте посмотрим формулу скалярного умножения:
Над,Nпредставляет любое число. Давайте посмотрим на пример. скалярNбудет 2, что означает, что каждый компонент вектора будет умножен на 2.
Реализация в Python:
Круто, давайте перейдем к следующей теме!
3. Точечный продукт
Чтобы рассчитать скалярное произведение двух векторов, сначала нужноумножить соответствующие элементы(x1поy1,x2поy2и тд) а потомсуммировать условия продукта,
Эта концепция на самом деле гораздо проще понять, когда вы видите общую формулу, так что вот она:
Теперь я запишу базовый пример с двумя векторами в 2-мерном пространстве:
Реализация в Python:
4. Векторная норма
Расчет состоит из 3 этапов:
Как вы можете себе представить, формула глупо проста:
А вот практический пример вектора в 2-мерном пространстве:
Реализация в Python:
5. Единица Вектор
Основная причина, по которой вы рассчитываете единичные векторы, заключается в том, что вы заботитесь только о направлении, а не о величине. Этот процесс нормализации включает в себя уменьшение величины, чтобы не искажать другие вычисления. [2]
Единичный вектор чаще всего обозначается символом шляпы (^) и вычисляется путем вычисления нормы, а затем деления каждого компонента вектора на норму.
Без лишних слов, вот формула:
В качестве примера я вычислю единичный вектор из произвольного трехмерного вектора:
Реализация в Python будет немного другой здесь. Здесь нетвстроенная функцияв Numpy для вычисления единичных векторов (по крайней мере, я не знаю об этом), но поскольку вы знаете формулу, процесс вычисления тривиален. Я объявил функцию, которая будет принимать вектор как вход, а затем возвращать этот вектор, деленный на его норму:
6. Угол между векторами
Это, вероятно, тема линейной алгебры, которая меня больше всего волнует. И причина в том, что я использую это здесь и там в моей повседневной работе для некоторых интересных вещей.
Расчет углов между векторами имеет много практических применений. Он широко используется вNLP(Обработка естественного языка) при поиске строк, которые очень похожи. Например, когдаTF-IDFиспользуется для некоторых текстовых данных, каждый ввод (попробуйте представить ввод как отдельный текст электронной почты) преобразуется в вектор.
Надеюсь, вы сможете увидеть потенциальные варианты использования в вашем проекте, если не будете беспокоиться об этом, вы увидите это в конце концов.
Вот формула для расчета угла. Ничего особенного, вы беретескалярное произведениедвух векторов и разделить это напроизведение норм:
И вот действительно простой пример двух произвольных трехмерных векторов:
И это в значительной степени заканчивает разговор о векторах.Разве это не плохо?
Вывод
Вот и все для некоторой основной сущности линейной алгебры для науки о данных, по крайней мере, когда речь идет о векторах. Следующая статья будет скрывать матрицы и будет немного длиннее этой.
Пока вы ждете, я настоятельно рекомендую вам проверить этот потрясающий канал на YouTube, в частности, этот плейлист. Это действительно глубоко встраивает интуицию в базовые и продвинутые понятия в линейной алгебре. Этот канал является моей честной рекомендацией, если вы знаете, как рассчитывать вещи, но на самом деле не знаете, почему вы делаете расчеты
Normalization using NumPy norm (Simple Examples)
Normalization of a vector or a matrix is a common operation performed in a variety of scientific, mathematical, and programming applications.
In this tutorial, we will understand what normalization is, and how to compute the same in Python.
We will look at the following topics on normalization using Python NumPy:
Introduction
NumPy arrays are most commonly used to represent vectors or matrices of numbers.
A 1-dimensional or a 1-D array is used for representing a vector and a 2-D array is used to define a matrix (where each row/column is a vector).
These vectors and matrices have interesting mathematical properties.
A vector, as we know it, is an entity in space. It has a magnitude and a direction.
Normalization of a vector is the transformation of a vector, obtained by performing certain mathematical operations on it. To perform normalization, we calculate a value called `norm` of a vector.
This value represents some property of the vector, for eg., an L2 norm of a vector denotes its length.
There are various types of norms, but in this tutorial, we are going to focus on the most popular ones namely the L2 norm and the L1 norm.
NumPy norm
NumPy has a dedicated submodule called linalg for functions related to Linear Algebra.
This submodule is a collection of Python functions used for performing various common Linear Algebraic operations such as vector products, eigenvalues calculation, determinant of a matrix, solving equations, etc.
Note that we will use the default value for the ord parameter for most of our code examples.
norm of an array
Let us now use the norm function to find the norm of a NumPy array.
Output:
Since the values in array a are 1,2,3,4 and 5, the L2 norm of the array has been calculated as:
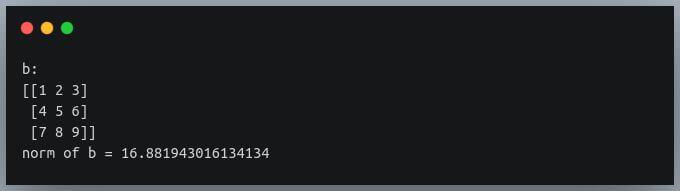
Let us now see how the function behaves on a matrix i.e a 2-D NumPy array.
Output:
As we can see, when we pass a matrix to the norm function, it still returns a single real value.
This is called the ‘Frobenius norm’ of a matrix. It is the square root of the sum of squares of all elements in the matrix.
Norms of columns and rows of a matrix
As we saw in the previous section, if we pass a matrix to the norm function, it calculates the sum of squares of all elements and returns a single value.
But often we need to normalize each column or row of a matrix separately. The row/columns of a matrix are, after all, 1-D vectors.
This can be achieved by specifying the ‘ axis ‘ parameter of the norm function.
For finding the norm of the columns, we pass the value 0 to the axis parameter, and for row norms, we pass the value 1.
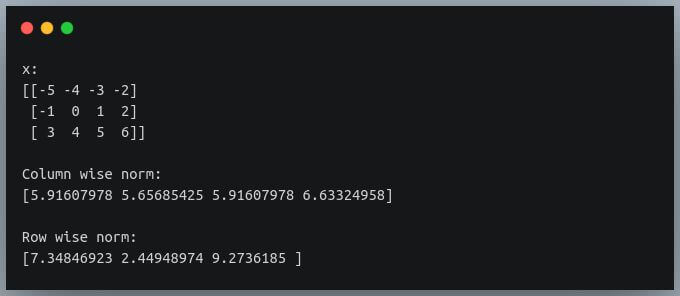
Let us look at examples of each of them.
Output:
Since there are 3 rows in our matrix, we get 3 norm values for row normalisation(axis=1)
Similarly, for each of the 4 columns, we get 4 norm values when we pass axis=0.
Norm of an n-dimensional array
We have so far seen the calculation of norms on vector and 2-D arrays. Let us now understand how to find the norm of n-dimensional arrays.
Let us construct a 3-dimensional array of the shape (10,2,2).
Output:
Now we can find the norm of this array, row-wise by passing the value of ‘axis’ as 0.
This will give us a matrix of size 2×2, each representing the norm of values in the for matrices at positions (0,0), (0,1), (1,0) and (1,2).
Output:
Why do we need norms?
As stated in the introduction, normalization is a very common operation in a variety of applications.
One important use of norm is to transform a given vector into a unit-length vector, that is, making the magnitude of vector = 1, while still preserving its direction.
This is achieved by dividing each element in a vector by its length i.e its L2-norm.
Normalization is also an important pre-processing step in many machine learning algorithms.
Let us normalize a vector and a matrix (a collection of vectors).
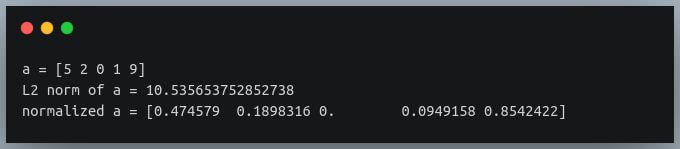
Output:
We now have a transformed vector whose length is 1. We can verify this by calculating the L2 norm of the normalized vector
Output:
Similarly, we can also normalize matrices.
This is especially useful when we need to normalize tabular data in a machine learning application, where each row represents a sample, and each column, an attribute or feature of the sample.
To normalize such data, we perform L2-normalization on the columns of the matrix i.e with axis = 0.
Let us suppose we have 5 samples of human data, where each sample represents a person’s height in cm, weight in kg, age in years, and monthly salary in USD.
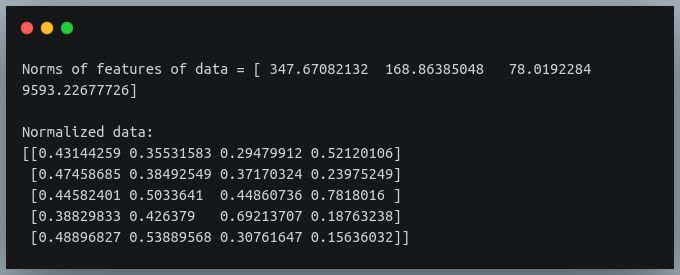
Let’s construct the matrix to represent this data.
In this example, we are representing 4 attributes of 5 individuals, and we need to normalize each of these attributes/features before feeding it to an ML algorithm.
Let us calculate the norms of each column, and then divide the respective columns by these norms.
Output:
L1 norm of a vector
Another popular type of norm is the L1 norm of a vector. It is equal to the sum of the magnitudes of elements of a vector.
Output:
As is evident, the sum of magnitudes of values in a (i.e sum of all absolute values in a) is equal to 13.
Note that another interesting use of these two norms i.e the L1 norm and the L2 norm is in the computation of loss in regularised gradient descent algorithms.
These are used in the famous ‘Ridge’ and ‘Lasso’ regression algorithms.
NumPy norm of arrays with nan values
While processing real-world data, we often encounter missing values or non-sensical for some features in data.
These values are called nan (Not a Number) for numeric features. They cannot be accounted for in any mathematical operation on the data.
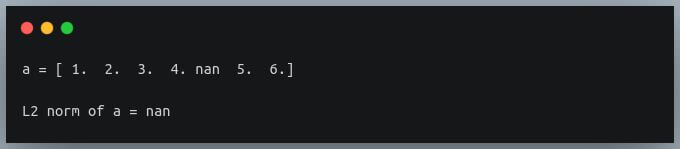
Let us take an example of a NumPy array with a nan value. We’ll compute the L2 norm on this array.
Output:
As can see, if we involve nan values when performing a mathematical operation, we are going to get a result that doesn’t make any sense i.e we end up with another nan value!
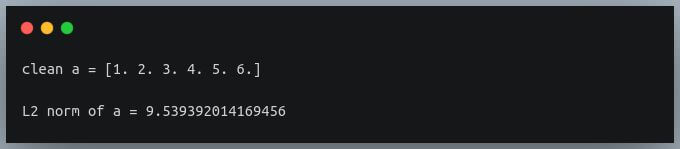
We can fix this by filtering out the nan values from the array and computing the norm on the rest of the array.
Output:
Euclidean distance using NumPy norm
You must have heard of the famous `Euclidean distance` formula to calculate the distance between two points A(x1,y1) and B(x2, y2)
Let us understand how this formula makes use of the L2 norm of a vector.
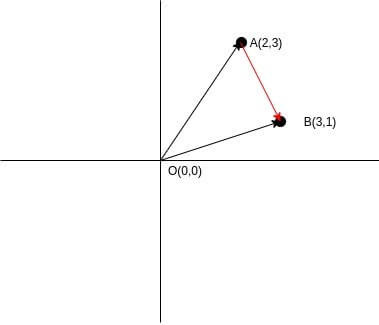
Let us consider two points A(2,3) and B(3,1). We need to find the distance between these two points.
Each of the two points can be represented as a vector from the origin to point.
We need to find the distance between points A and B, i.e the length of vector AB.
By property of vector addition, vector AB = OA – OB = B – A.
Now, all we have to do is find the length of this vector AB, which is nothing but the L2 norm of vector AB!
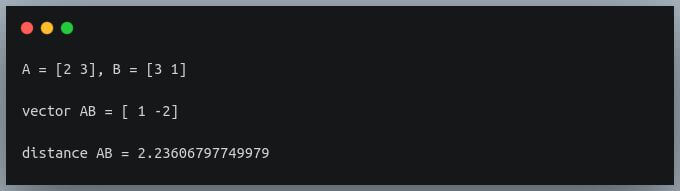
Let’s code this in Python.
Output:
We get the distance between A and B as 2.236, which we can verify using the Euclidean distance formula.
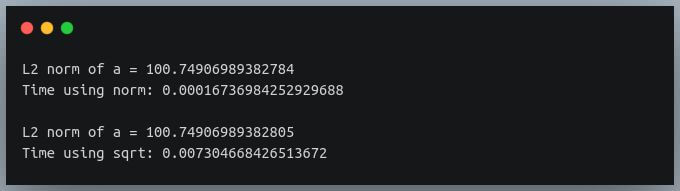
Performance comparison: NumPy norm vs sqrt
Let’s compare the time performance of the two methods.
Output:
The norm method is much faster (about 50 times faster) than the np.sqrt method on an array of 10000 values.
Conclusion
In this tutorial, we understood what norms of vectors and matrices are, and how to calculate them using NumPy’s norm method
We also saw how we can compute norms of individual rows and columns of a matrix.
We understood the need for computing norms and their applications in vector algebra and machine learning.
For most of the tutorial, we focused on L2 norms. We also introduced another popular norm called the ‘L1 norm’ and computed the same using NumPy norm.
We then learned how to compute norms of arrays with nan values.
Next, we saw how norms are related to the Euclidean distance formula and calculated the distance between two points using NumPy norm.
Finally, we compared the performance of the norm method with NumPy’s sqrt method for computing the L2 norm of an array.
Machine Learning Engineer & Software Developer working on challenging problems in Computer Vision at IITK Research and Development center.
3+ years of coding experience in Python, 1+ years of experience in Data Science and Machine Learning.
Skills: C++, OpenCV, Pytorch, Darknet, Pandas, ReactJS, Django.