pmax что такое в электрике
Что такое электрическая мощность

Транспортировка или передача больших электрических мощностей в промышленных целях выполняется по высоковольтным линиям электропередач.
Преобразование электрической энергии осуществляется на трансформаторных подстанциях.
Потребление электричества происходит в бытовых и промышленных устройствах различного назначения. Одним из распространенных их видов являются лампы накаливания различных номиналов.
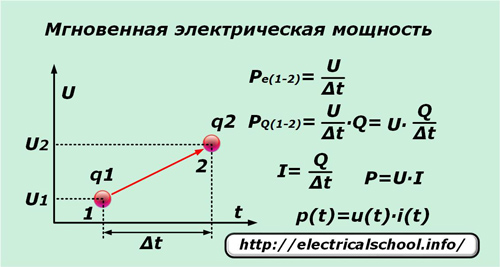
Определение мгновенной электрической мощности
В теоретической электротехнике для вывода основных соотношений между током, напряжением и мощностью используются их представления в виде мгновенных величин, которые фиксируются в какой-то определенный временной момент.
Если за очень короткий промежуток времени ∆t единичный элементарный заряд q под действием напряжения U перемещается из точки «1» в точку «2», то он совершает работу, равную разности потенциалов между этими точками. Разделив ее на промежуток времени ∆t, получим выражение мгновенной мощности для единичного заряда Pe(1-2).
Поскольку под действием приложенного напряжения перемещается не только единичный заряд, а все соседние, оказавшиеся под влиянием этой силы, количество которых удобно представить числом Q, то для них можно записать мгновенную величину мощности PQ(1-2).
Выполнив простые преобразования получим выражение мощности Р и зависимость ее мгновенного значения p(t) от составляющих произведения мгновенного тока i(t) и напряжения u(t).
Определение электрической мощности постоянного тока
В цепях постоянного тока величина падения напряжения на участке цепи и протекающего по нему тока не изменяется и остается стабильной, равной мгновенным значениям. Поэтому определить мощность в этой схеме можно перемножением этих величин или делением совершенной работы А на период времени ее выполнения, как показано на поясняющей картинке.
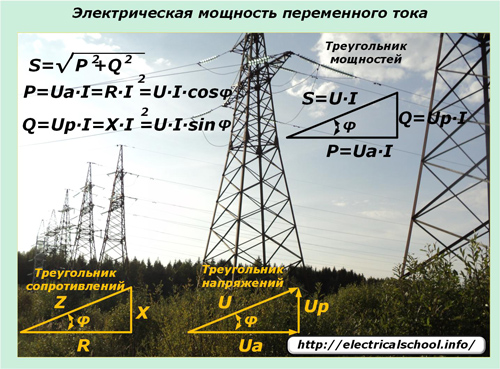
Определение электрической мощности переменного тока
Законы синусоидального изменения токов и напряжений, передаваемых по электрическим сетям, накладывают свое влияние на выражение мощности в таких цепях. Здесь действует полная мощность, которая описывается треугольником мощностей и состоит из активной и реактивной составляющих.
Электрический ток синусоидальный формы при прохождении по линиям электропередач со смешанными видами нагрузок на всех участках не изменяет форму своей гармоники. А падение напряжения на реактивных нагрузках сдвигается по фазе в определенную сторону. Понять влияние приложенных нагрузок на изменение мощности в цепи и ее направление помогают выражения мгновенных величин.
При этом сразу обратите внимание на то, что направление прохождения тока от генератора к потребителю и передаваемой мощности по созданной цепи — это совершенно разные вещи, которые в отдельных случаях могут не только не совпадать, но и направлены в противоположные стороны.
Рассмотрим эти взаимосвязи при их идеальном, чистом проявлении для разных видов нагрузок:
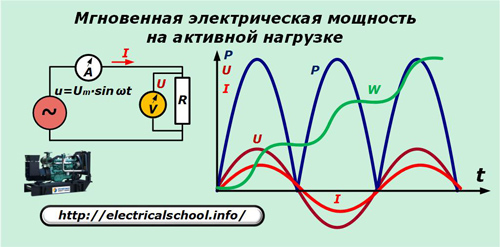
Выделение мощности на активной нагрузке
Будем считать, что генератор вырабатывает идеальную синусоиду напряжения u, которая прикладывается к чисто активному сопротивлению цепи. Амперметр А и вольтметр V замеряют ток I и напряжение U в каждый момент времени t.
На графике видно, что синусоиды тока и падения напряжения на активном сопротивлении совпадают по частоте и фазе, совершая одинаковые колебания. Мощность же, выражаемая их произведением, колеблется с удвоенной частотой и всегда остается положительной.
p=u∙i=Um∙sinωt∙Um/R∙sinωt=Um 2 /R∙sin 2 ωt=Um 2 /2R∙(1-cos2ωt).
Если перейти к выражению действующего напряжения, то получим: p=P∙(1-cos2ωt).
Далее проинтегрируем мощность за период одного колебания Т и сможем заметить, что приращение энергии ∆W за этот промежуток увеличивается. С дальнейшим течением времени активное сопротивление продолжает потреблять новые порции электроэнергии, как показано на графике.
На реактивных нагрузках характеристики потребляемой мощности отличаются, имеют другой вид.
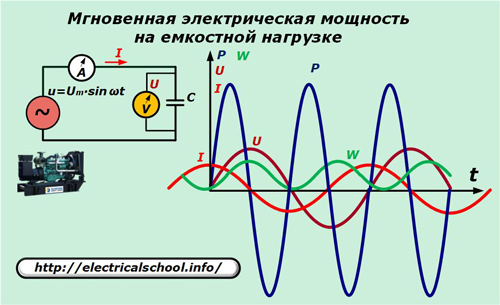
Выделение мощности на емкостной нагрузке
В схеме питания генератора заменим резистивный элемент конденсатором с емкостью С.
Соотношения между током и падением напряжения на емкости выражаются зависимостью: I=C∙dU/dt=ω∙C ∙Um∙cosωt.
Перемножим значения мгновенных выражений тока с напряжением и получим значение мощности, которая потребляется емкостной нагрузкой.
p=u∙i=Um∙sinωt∙ωC ∙Um∙cosωt=ω∙C ∙Um 2 ∙sinωt∙cosωt=Um 2 /(2Xc)∙sin2ωt=U 2 /(2Xc)∙sin2ωt.
Здесь видно, что мощность совершает колебания относительно нуля с удвоенной частотой приложенного напряжения. Суммарное ее значение за период гармоники, как и приращение энергии, равно нулю.
Это означает, что энергия перемещается по замкнутому контуру цепи в обе стороны, но никакой работы не совершает. Подобный факт объясняется тем, что при нарастании напряжения источника по абсолютной величине мощность положительна, а поток энергии по цепи направляется в емкость, где происходит накопление энергии.
После того как напряжение переходит на падающий участок гармоники, из емкости начинается возврат энергии в контур к источнику. В обоих этих процессах полезная работа не совершается.
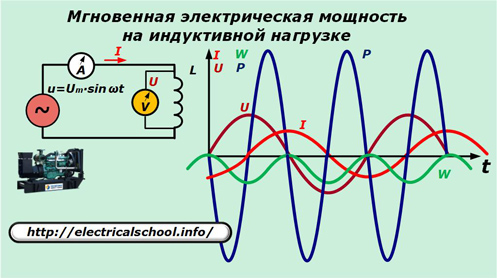
Выделение мощности на индуктивной нагрузке
Теперь в схеме питания заменим конденсатор индуктивностью L.
Здесь ток через индуктивность выражается соотношением:
p=u∙i=Um∙sinωt∙ωC ∙(-Um/ωL∙cosωt)=-Um 2 /ωL∙sinωt∙cosωt=-Um 2 /(2XL)∙sin2ωt=-U 2 /(2XL)∙sin2ωt.
Полученные выражения позволяют увидеть характер изменения направления мощности и приращения энергии на индуктивности, которые совершают такие же бесполезные для выполнения работы колебания, как и на емкости.
Выделяемую на реактивных нагрузках мощность называют реактивной составляющей. Она в идеальных условиях, когда у соединительных проводов нет активного сопротивления, кажется безобидной и не создает никакого вреда. Но в условиях реального электроснабжения периодические прохождения и колебания реактивной мощности вызывают нагрев всех активных элементов, включая соединительные провода, на который затрачивается определенная энергия и снижается величина приложенной полной мощности источника.
Основное отличие реактивной составляющей мощности состоит в том, что она вообще не совершает полезной работы, а ведет к потерям электрической энергии и превышению нагрузок оборудования, особенно опасных в критических ситуациях.
По этим причинам для устранения влияния реактивной мощности используются специальные технические системы ее компенсации.
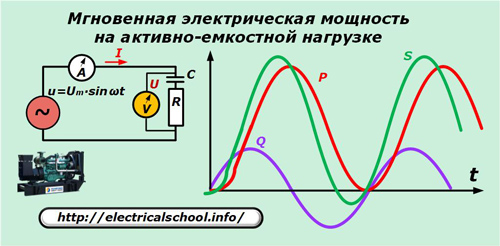
Выделение мощности на смешанной нагрузке
В качестве примера используем нагрузку на генератор с активно емкостной характеристикой.
На приведенном графике не показаны для упрощения картины синусоиды токов и напряжений, но следует учесть, что при активно-емкостном характере нагрузки вектор тока опережает напряжение.
После преобразований получим: p=P∙(1- cos 2ωt)+Q ∙sin2ωt.
Эти два слагаемые в последнем выражении являются активной и реактивной составляющими мгновенной полной мощности. Только первая из них совершает полезную работу.
Приборы измерения мощности
Для анализа потребления электроэнергии и расчета за нее используются приборы учета, которые давно получили название «счетчики». Их работа основана на измерении действующих величин тока и напряжения и автоматическом перемножении их с выводом информации.
Счетчики отображают потребляемую мощность с учетом времени работы электроприборов по нарастающему принципу от момента включения электросчетчика под нагрузку.
Для замера в цепях переменного тока активной составляющей мощности используются ваттметры, а реактивной — варметры. Они имеют разные обозначения единиц измерения:
Чтобы определить полную мощность потребления, необходимо по формуле треугольника мощностей вычислить ее величину на основе показаний ваттметра и варметра. Она выражается в своих единицах — вольт-амперах.
Принятые обозначения единиц каждой помогают электрикам судить не только о ее величине, но и о характере составляющей мощности.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Что такое активная и реактивная мощность переменного электрического тока?
Все мы ежедневно сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической инструкции указана мощность. Сегодня мы разберемся что же это такое, узнаем виды и способы расчета.
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.
В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).
Рассчитывается по формуле: P = U⋅I⋅cosφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.
ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73
Понятие реактивной мощности
Реактивная «вредная» мощность — это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.
Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.
Обозначается эта величина латинской буквой Q.
ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).
Рассчитывается по формуле:
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.
ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.
Емкостные и индуктивные нагрузки
Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.
Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.
ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.
Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.
ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.
Коэффициент мощности cosφ
Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.
Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.
ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.
Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.
Понятие полной мощности. Треугольник мощностей
Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.
Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.
ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).
Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.
Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.
Как найти активную, реактивную и полную мощности. Пример расчета
Все расчеты строятся на указанных ранее формулах и треугольнике мощностей. Давайте рассмотрим задачу, наиболее часто встречающуюся на практике.
Обычно на электроприборах указана активная мощность и значение коэффициента cosφ. Имея эти данные несложно рассчитать реактивную и полную составляющие.
Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.
Далее, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.
Как измеряют cosφ на практике
Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.
Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.
Как перевести амперы в ватты и обратно?
Как перевести амперы в киловаты?
Как рассчитать падение напряжения по длине кабеля в электрических сетях
Что такое коэффициент трансформации трансформатора?
Способы вычисления потребления электроэнергии бытовыми приборами
Что такое делитель напряжения и как его рассчитать?
Еще раз про мощность: активную, реактивную, полную
(P, Q, S), а также коэффициент мощности (PF)
Из письма клиента:
Подскажите, ради Бога, почему мощность ИБП указывается в Вольт-Амперах, а не в привычных для всех киловаттах. Это сильно напрягает. Ведь все уже давно привыкли к киловаттам. Да и мощность всех приборов в основном указана в кВт.
Алексей. 21 июнь 2007
В технических характеристиках любого ИБП указаны полная мощность [кВА] и активная мощность [кВт] – они характеризуют нагрузочную способность ИБП. Пример, см. фотографии ниже:
Мощность не всех приборов указана в Вт, например:
Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.
Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность и реактивная мощность точно характеризуют нагрузку.
Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности. Все эти 4 параметра:
Эти параметры связаны соотношениями: S*S=P*P+Q*Q, cosФ=k=P/S
Также cosФ называется коэффициентом мощности (Power Factor – PF)
Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.
То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.
Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
См. учебники по электротехнике, например:
Так же см. AC power, Power factor, Electrical resistance, Reactance http://en.wikipedia.org
(перевод: http://electron287.narod.ru/pages/page1.html)
Приложение
Пример 1: мощность трансформаторов и автотрансформаторов указывается в ВА (Вольт·Амперах)
Трансформаторы питания номинальной выходной мощностью 25-60 ВА
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП)
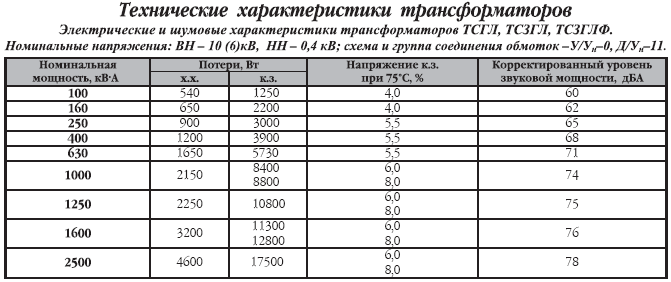
http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)
| Однофазные автотрансформаторы | ||
| TDGC2-0.5 kVa, 2A | АОСН-2-220-82 | |
| TDGC2-1.0 kVa, 4A | Латр 1.25 | АОСН-4-220-82 |
| TDGC2-2.0 kVa, 8A | Латр 2.5 | АОСН-8-220-82 |
| TDGC2-3.0 kVa, 12A | ||
| TDGC2-4.0 kVa, 16A | ||
| TDGC2-5.0 kVa, 20A | АОСН-20-220 | |
| TDGC2-7.0 kVa, 28A | ||
| TDGC2-10 kVa, 40A | АОМН-40-220 | |
| TDGC2-15 kVa, 60A | ||
| TDGC2-20 kVa, 80A | ||
http://www.gstransformers.com/products/voltage-regulators.html (ЛАТР / лабораторные автотрансформаторы TDGC2)
Пример 2: мощность конденсаторов указывается в Варах (Вольт·Амперах реактивных)
http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК)
Пример 3: технические данные электромоторов содержат активную мощность (кВт) и cosФ
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР)
http://www.weiku.com/products/10359463/Stainless_Steel_cutting_machine.html
(комбинированная нагрузка – станок плазменной резки стали / Inverter Plasma cutter LGK160 (IGBT)
Технические данные разрядных ламп содержат активную мощность (кВт) и cosФ
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ)
http://www.silverstonetek.com.tw/product.php?pid=365&area=en (блок питания ПК)
Дополнение 1
Поэтому во многих странах приняты стандарты нормирующие коэффициент мощности оборудования.
Дополнение 2
Дополнение 3. Важное замечание относительно коэффициента мощности ИБП и стабилизаторов напряжения
Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8.
В стабилизаторах напряжения дело обстоит иначе. Для стабилизатора коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
Дополнение 4
Наглядные примеры чистой активной и чистой реактивных нагрузок:
=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Дополнение 5
Для обозначения преобладающего реактивного сопротивления (индуктивного либо ёмкостного) коэффициенту мощности приписывается знак:
+ (плюс) – если суммарное реактивное сопротивление является индуктивным (пример: PF=+0.5). Фаза тока отстаёт от фазы напряжения на угол Ф.
— (минус) – если суммарное реактивное сопротивление является ёмкостным (пример: PF=-0,5). Фаза тока опережает фазу напряжения на угол Ф.
Дополнение 6
В различных областях техники мощность может быть либо полезной, либо паразитной НЕЗАВИСИМО от того активная она или реактивная. Например, необходимо различать активную полезную мощность рассеиваемую на рабочей нагрузке и активную паразитную мощность рассеиваемую в линии электропередачи. Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.
Дополнительные вопросы
Вопрос 1:
Почему во всех учебниках электротехники при расчете цепей переменного тока используют мнимые числа / величины (например, реактивная мощность, реактивное сопротивление и др.), которые не существуют в реальности?
Ответ:
Да, все отдельные величины в окружающем мире – действительные. В том числе температура, реактивное сопротивление, и т.д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].
Замечание:
Раньше в физике использовались только одиночные величины и при расчете все математические величины соответствовали реальным величинам окружающего мира. Например, расстояние равно скорость умножить на время (S=v*t). Затем с развитием физики, то есть по мере изучения более сложных объектов (свет, волны, переменный электрический ток, атом, космос и др.) появилось такое большое количество физических величин, что рассчитывать каждую в отдельности стало невозможно. Это проблема не только ручного вычисления, но и проблема составления программ для ЭВМ. Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:
Вопрос 2:
На странице http://en.wikipedia.org/wiki/Ac_power показаны S P Q Ф на комплексной, то есть мнимой / несуществующей плоскости. Какое отношение это все имеет к реальности?
Ответ:
Проводить расчеты с реальными синусоидами сложно, поэтому для упрощения вычислений используют векторное (комплексное) представление как на рис. выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.
Вопрос 3:
Обычными токовыми клещами и мультиметром измерен ток нагрузки 10 A, и напряжение на нагрузке 225 В. Перемножаем и получаем мощность нагрузки в Вт: 10 A · 225В = 2250 Вт.
Ответ:
Вы получили (рассчитали) полную мощность нагрузки 2250 ВА. Поэтому ваш ответ будет справедлив только, если ваша нагрузка чисто активная, тогда действительно Вольт·Ампер равен Ватту. Для всех других типов нагрузок (например электромотор) – нет. Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:
См. дополнительную литературу, например:
[4]. AC power, Power factor, Electrical resistance, Reactance
http://en.wikipedia.org (перевод: http://electron287.narod.ru/pages/page1.html)
[5]. Теория и расчёт трансформаторов малой мощности Ю.Н.Стародубцев / РадиоСофт Москва 2005 г. / rev d25d5r4feb2013
[6]. Международная система единиц, СИ, см напр. ГОСТ 8.417-2002. ЕДИНИЦЫ ВЕЛИЧИН