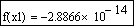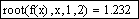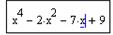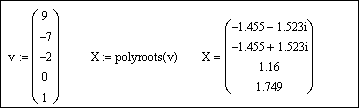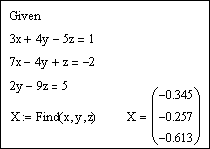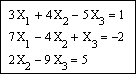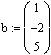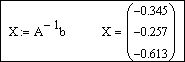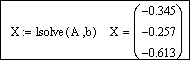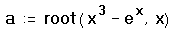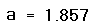root mathcad что делает

Иллюстрированный самоучитель по MathCAD 12

Уравнение с одним неизвестным: функция root

Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.

Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.

Листинг 5.13. Два варианта уравнения методом секущих:

Как вы можете убедиться (первая строка листинга 5.13), для решения уравнения при помощи функции root (f (x),x,a,b) не требуется задавать начального приближения, а достаточно указать интервал [а,b]. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Когда root имеет четыре аргумента, следует помнить о двух ее особенностях. Во-первых, внутри интервала не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно. Во-вторых, значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были «хорошими», т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.

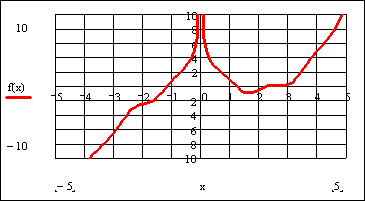
Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.

Источник

Root mathcad что делает

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

Этот прием используется в Mathcad так:

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

Задание 1. Решить уравнение .

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .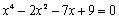

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений 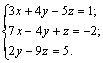Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

Источник

Root mathcad что делает

8.1. Одно уравнение с одним неизвестным

Рассмотрим одно алгебраическое уравнение с одним неизвестным х.

Для решения таких уравнений Mathcad имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.

Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.

Приведем пример решения очень простого уравнения sin(x)=o, корни которого известны заранее.

Листинг 8.1. Поиск корня нелинейного алгебраического уравнения

Рис. 8.1. Графическое решение уравнения sin(x)=0

График функции f (x)=sin(x) и положение найденного корня показаны на рис. 8.1. Обратите внимание, что, хотя уравнение имеет бесконечное количество корней xn=npi (n=0,±1,±2. ), Mathcad находит (с заданной точностью) только один из них, х0, лежащий наиболее близко к х=0.5. Если задать другое начальное значение, например х=3, то решением будет другой корень уравнения х1=pi и т. д. Таким образом, для поиска корня средствами Mathcad требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих и состоит в следующем (рис. 8.2):

Листинг 8.3. Поиск мнимого корня

Для решения этого уравнения второй вид функции root (с четырьмя, а не с двумя аргументами) неприменим, поскольку f (х) является положительноопределенной, и указать интервал, на границах которого она имела бы разный знак, невозможно.

Листинг 8.4. Поиск корня уравнения, заданного функцией двух переменных

Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 8.8.

Источник

Встроенные функции MathCAD для решения нелинейных алгебраических и трансцендентных уравнений

Уравнения в MathCAD решаются с помощью двух встроенных функцийroot и polyroots.

3.1.2.1 Встроенная функция MathCAD – root(F(x), x)

Для численного решения уравнений предназначена стандартная функция MathCAD – root(F(x), x), которая возвращает значение корня с заданной точностью. Функция root имеет два аргумента:

первый – выражение, стоящее в левой части уравнения, то есть F(x), второй – переменная, относительно которой решается уравнение, то есть x.

Ищется значение переменной x, при которой выражение F(x) обращается в ноль. Функция root возвращает значение переменной x, которая обращает выражение F(x) в ноль.

Функция реализует вычисление итерационным методом и перед её применением необходимо задать начальное значение переменной x, принадлежащее интервалу изоляции корня.

В зависимости от начального приближения функция root возвращает различные значения.

Решение уравнений с помощью функции root может производиться с различной точностью, которая задается значением системной переменной TOL.

Пример 3.1 Решить уравнение с точностью .

Процесс решения показан на рисунке 1. Выполняется следующая последовательность действий:

1.Сначала вводится функция 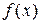, соответствующая левой части уравнения.

2. Задается точность.

3. Графически находится приближенное решение уравнения (можно использовать трассировку).

4. При помощи функции root выполняется нахождение решения уравнения с заданной точностью.

5. Выполняется проверка найденного решения.

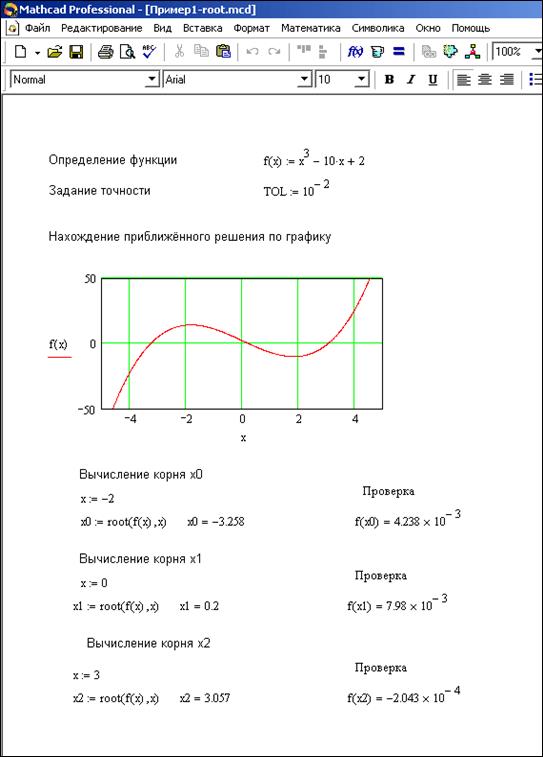
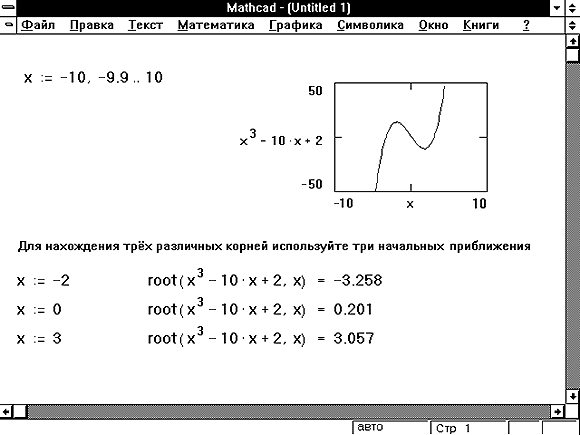
В зависимости от начального приближения функция root возвращает различные значения. Результат решения задачи приведён на рисунке 3.1.1 В результате найдены корни x0=-3.258, x1=0.2, x2=3.057.

Рисунок 3.1.1 – Пример решения нелинейного алгебраического уравнения

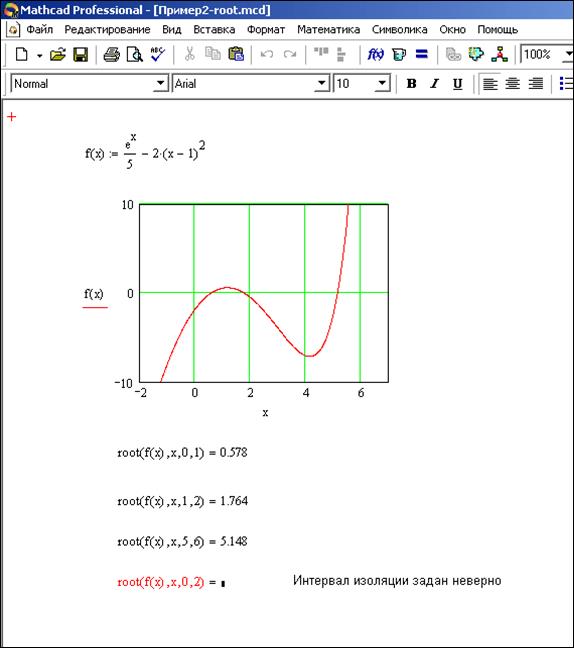
Результаты решения показаны на рисунке 2. Используя график функции, определяют пределы интервала изоляции каждого корня, а затем с помощью функции root (f(x), x, a, b) находят значение интересующего корня.

В данном случае найдено три корня. Необходимо правильно указывать интервал изоляции, в случае ошибки значение корня не будет найдено, что показано на рисунке 3.1.2

Рисунок 3.1.2 – Пример решения уравнения с использованием

функции root (f(x), x, a, b)

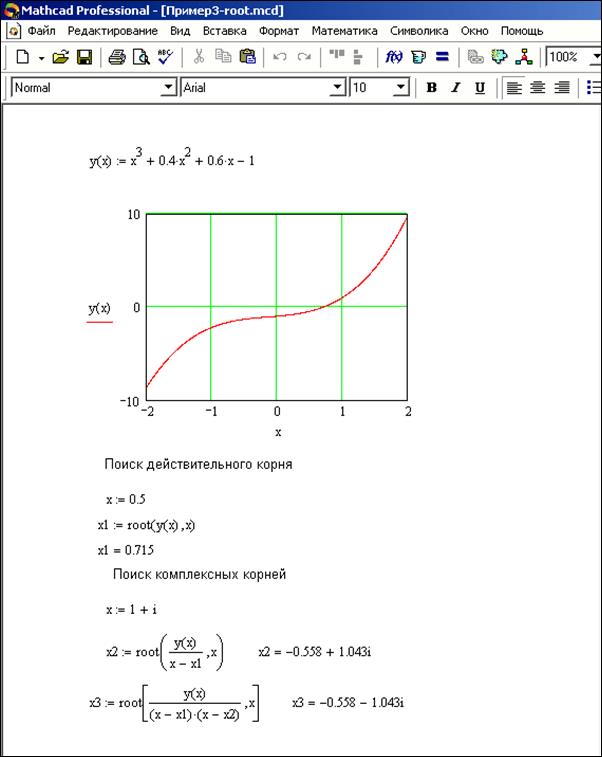
На рисунке 3.1.3 показан пример решения уравнения, имеющего комплексные корни. В таких случаях начальное приближённое значение корня также должно быть комплексным. При вводе мнимого числа надо писать 1i, а не i. В данном примере при вычислении второго корня х2 первый исключается делением f(х) на (х-х1). При нахождении третьего корня f(х) делится на (х-х1)(х-х2).

Рисунок 3.1.3 – Пример решения уравнения, имеющего

действительные и комплексные корни

Необходимо отметить особенность функции root, связанную с тем, что она не всегда позволяет найти значение корня.

Mathcad при поиске корня с помощью функции root использует метод итераций. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным и функция root возвращает результат. Если после многих итераций Mathcad не может найти соответствующее приближение, то появляется сообщение об ошибке «отсутствует сходимость». Эта ошибка может быть вызвана следующими причинами:

— уравнение не имеет корней;

— корни уравнения располагаются далеко от начального приближения;

— выражение имеет локальные максимумы или минимумы между начальным приближением и корнем;

— выражение имеет разрывы между начальным приближением и корнями;

— выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).

Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному решению.

Источник

Root mathcad что делает

Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.

Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 1: Использование графика и функции root для поиска корней уравнения.

Что делать, когда функция root не сходится

Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find

Некоторые советы по использованию функции root

Решение уравнений с параметром

Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции

Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.

Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.

Рисунок 2: Определение функции пользователя с функцией root.

Нахождение корней полинома

Для нахождения корней выражения, имеющего вид

лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.

Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.

Рисунок 4: Использование функции polyroots для поиска корней полинома.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник