rsa ключ что это такое

Что такое RSA-ключ ЕГАИС?

Регулятор закона в целях контроля передвижения каждой бутылки алкоголя от производства до покупателя внедрил всероссийскую базу данных. Это обеспечивает прозрачность движения каждой единицы товара, а также помогает бороться с недоимками по фискальным платежам. Для работы в системе ЕГАИС требуется иметь крипто-ключ и сформированный ключ RSA, а также транспортный модуль. Все это необходимо для защищенной работы в системе, чтобы третьи лица не смогли воспользоваться информацией в своих интересах.

Ключ RSA ЕГАИС – что это?

Представляет собой сертификат для защищенного соединения с единой платформой. Система необходима для передачи данных в безопасном режиме. Криптосистема позволяет пользоваться ключом шифрования только соответствующим зарегистрированным субъектам. Все данные зашифрованы от посторонних третьих лиц. РСА-ключ для ЕГАИС записывается на крипто-ключ на веб-ресурсе официального портала. Операция по записи зашифрованных данных предоставляется бесплатно.

В процессе осуществления профессиональной деятельности для каждого юридического подразделения необходимо получить собственный RSA-ключ для работы с использованием Рутокен в ЕГАИС. Перед тем как зарегистрировать соответствующие данные требуется удостовериться, что запущен аппаратный крипто-ключ той компании, для которой формируется сертификат РСА.

Что нужно для формирования ключа RSA ЕГАИС Рутокен

На начальной стадии пользователю потребуется зарегистрироваться на официальном ресурсе. После этого понадобится зайти в Личный кабинет с помощью уже имеющейся электронной подписи. В панели управления необходимо будет выбрать графу «Показать сертификат». После чего вы сможете увидеть все сертификационные материалы со сведениями о ваших точках с указанием всех идентификационных данных. Представленная информация необходима для записи специального RSA-ключа.

На следующем этапе нужно будет перейти в раздел «Получить ключ». На табло вы сможете увидеть перечень пунктов сбыта АП, которые были указаны вами при прохождении процедуры регистрации. Затем вы можете выбрать соответствующий пункт, для которого предназначен специализированный крипто-ключ и выбрать поле «Сформировать ключ». Электронная платформа запросит ввести пароль. В случае какого-либо затруднения вы можете обратиться в службу поддержки на официальном веб-ресурсе.

После того как вы установили или перезаписали РСА сертификат ЕГАИС на Рутокен можно приступать к установке УТМ. Запустив универсальный транспортный модуль, вы сможете приступить к производству и продаже алкоголя в рамках новых положений законодателя. Дополнительно нужно будет позаботиться о приобретении сканеров с целью считывания данных и стабильного осуществления всех процессов на электронной платформе.

Как обновить сертификат РСА ЕГАИС Рутокен

В связи с обновлением сертификата все субъекты алкорынка обязаны произвести обновление ключа RSA. В самом начале необходимо будет удалить старый сертификат и уже затем установить новый.

После удаления необходимо произвести обновление ключа RSA ЕГАИС Рутокен. Все манипуляции нужно будет выполнить на официальном веб-портале. При формировании ключа вам нужно будет ввести пин-код. Если все идентификационные данные будут введены правильно, сертификат будет зарегистрирован. В случае возникновения каких-либо сложностей при продлении ключа РСА ЕГАИС обратитесь в техподдержку. Специалисты могут подключиться удаленно к вашему компьютерному устройству в целях наиболее оперативного решения вопроса.

Ошибки с RSA-ключом ЕГАИС

В процессе генерации РСА сертификата могут возникать определенные сложности. В большинстве случаев существуют две причины. Первая – это неполадки на веб-ресурсе. Вторая – некорректные настройки компьютерного оборудования. Для устранения проблем с RSA-ключом ЕГАИС потребуется выполнить следующие действия:

Если же при обновлении ключа RSA ЕГАИС возникнут какие-либо сложности и не будет появляться графа «Запрос пин-кода», то необходимо в компьютерном оборудовании произвести соответствующие корректировки в настройках. В большинстве случаев неправильные настройки являются следствием невыполнения операций по формированию ключа.

При работе с использованием системы RuToken вам потребуется зайти в Панель управления, где потребуется выбрать Настройки, напротив строки Рутокен вам необходимо выбрать значение Microsoft Base Smart Card Crypto Provider. После этого нужно попробовать еще раз сформировать ключ. Если возникнут сложности, необходимо произвести обновление драйверов.

Помимо этого, проблема возникает при неправильном введении пин-кода. Если вы несколько раз неправильно ввели данные, то носитель может заблокироваться. Тогда вам придется обратиться в удостоверяющий центр. Дополнительно причиной ошибки может стать несоответствие адреса РСА ключа, указанного в лицензии. Если же будет выявление несоответствие данных, нужно будет обратиться в техподдержку Росалкогольрегулирования. С соответствующим запросом можно обратиться как лично, так и через Личный кабинет. Стоит отметить, что в некоторых случаях после внесения корректировок может потребоваться повторное формирование РСА-ключа.

Итак, для успешной работы во всероссийской системе вам помимо крипто-ключа и установки УТМ необходимо позаботиться о формировании RSA-ключа.

Источник

RSA, а так ли все просто?

Прелюдия

Немного теории

Для того чтобы понять почему крайне не рекомендуется использовать RSA в его наиболее простой форме сперва отметим следующее требование, выдвигаемое к асимметричным криптосистемам.
Требование 1:
Современная асимметричная криптосистема может(но это еще не факт) считаться стойкой, если злоумышленник, имея два открытых текста M₁ и M₂, а также один шифротекст C_b не может с вероятностью большей, чем 0.5 определить какому из двух открытых текстов соответствует шифротекст C_b.
Посмотрим, удовлетворяет ли RSA данному требованию. Итак, представим, злоумышленник Мэлори прослушивает переписку Алисы и Боба. В один чудесный для себя день он видит, что Боб в открытом виде задал Алисе очень важный вопрос, знание ответа на который обогатит, ну или, по крайней мере, безмерно потешит любопытство Мэлори. Алиса односложно отвечает Бобу на этот вопрос личного характера. Она шифрует свой ответ открытым ключом Боба и отправляет шифротекст. Далее Мэлори перехватывает шифротекст и подозревает, что в нем зашифровано либо «Да», либо «Нет». Всё, что ему теперь нужно сделать для того чтобы узнать ответ Алисы это зашифровать открытым ключом Боба слово «Да» и если полученный криптотекст совпадет с перехваченным, то это означает, что Алиса ответила «Да», в противном же случает злоумышленник поймет, что ответом было «Нет».

Как видно из этого, пускай несколько надуманного, но все же не столь и утопичного примера, RSA не столь надежна как это принято считать. Да конечно, можно сказать, что Алиса сама дура и никто ее не просил отвечать на такой серьезный для нее вопрос односложно. Так что же теперь запретить использование односложных ответов в криптографии? Конечно, нет. Все не так плохо, достаточно чтобы алгоритм добавлял к тексту некоторую случайную информацию, которую бы невозможно было предугадать и коварный Мэлори будет бессилен. Ведь, в самом деле, не сможет же он предсказать, что ответ «Да» после обработки алгоритмом превратится, например, в «Да4FE6DA54», а следовательно и зашифровать это сообщение он не сможет и нечего ему будет сравнивать с перехваченным криптотекстом.

Таким образом, уже сейчас можно сказать, что RSA во всех своих проявлениях будь то PGP или SSL не шифрует только отправленные на вход шифрующей функции данные. Алгоритм сперва добавляет к этим данным блоки содержащие случайный набор бит. И только после этого полученный результат шифруется. Т.е. вместо привычной всем
C=M E (mod N)
получаем более близкую к действительности
C=(M||Rand) E (mod N),
где Rand случайное число.
Такую методику называют схемами дополнения. В настоящее время использование RSA без схем дополнения является не столько плохим тоном, сколько непосредственно нарушением стандартов.

Но это далеко не все. Считается, что даже если криптоситема удовлетворяет сформулированному выше требованию, это еще не доказывает ее пригодность в практических целях. Сформулируем еще одно требование к стойкости асимметричного алгоритма.

Требование 2:
Пусть злоумышленник имеет доступ к расшифровывающему «черному ящику». Т.е. любой криптотекст по просьбе злоумышленника может быть расшифрован. Далее злоумышленник создает два открытых текста M₁ и M₂. Один из этих текстов шифруется и полученный в результате криптотекст C_b возвращается злоумышленнику. Задача злоумышленника угадать с вероятностью большей чем 0.5 какому из сообщений M₁ и M₂ соответсвует криптотекст C_b. При этом он может попросить расшифровать любое сообщение, кроме C_b(в противном случае игра не имеет смысла). Говорят что криптосистема стойкая, если злоумышленник, даже в таких прекрасных для себя условиях, не сможет указать какому исходному тексту соответствует C_b с вероятностью большей 0.5.

В свете вышесказанного посмотрим как с этим обстоят дела в RSA.
Итак, злоумышленник имеет два сообщения M₁ и M₂. А также криптотекст
C_b=M₁ E (mod N).
Ему необходимо указать какому конкретно из двух текстов соответствует C_b. Для этого он может предпринять следующее. Зная открытый ключ E, он может создать сообщение
C’=2 E *C_b(mod N).
Далее он просит расшифровывающий «черный ящик» расшифровать сообщение C’. А затем несложная арифметика ему в помощь. Имеем:
M’=C’ D (mod N)=2 ED *M₁ ED (mod N)=2*M₁(mod N).
Т.е. вычислив M’/2 злоумышленник увидит M₁. А это означает, что он поймет что в нашем примере было зашифровано сообщение M₁, а следовательно мы еще раз убедились в неприемлемости использования RSA в его наивном виде на практике.

Устранить и эту неприятность помогают схемы дополнения. Только теперь к ним выдвигается требование не только о том, чтобы дополнительная информация была абсолютно случайной и непрогнозируемой. Но так же и том, чтобы дополнительные блоки помогали определить был ли шифротекст получен в результате работы шифрующей функции или он смоделирован злоумышленником. Причем в случае, если будет обнаружено, что шифротекст смоделирован вместо расшифрованных данных атакующему будет выдано сообщение о несоответствие данных реальному криптотексту.

Казалось бы, реализация такой схемы дополнения является труднорешаемой задачей, но ведь в криптографии уже есть готовый инструмент контроля целостности данных. Конечно же, это хеш-функции. Все современные схемы дополнений реализованы на идее применения хеш-функции в качестве проверки расшифрованных данных на подлинность.

В RSA при подписи и при шифровании данных используют две различные схемы дополнений. Схема, реализуемая для подписания документов, называется RSA-PSS(probabilistic signature scheme) или вероятностная схема подписи. Схема, используемая при шифровании – RSA-OAEP(Optimal asymmetric encryption padding) или оптимизированное асимметричное дополнение шифрования, на примере OAEP и рассмотрим как на самом деле происходит шифрование сообщений в RSA.

RSA-OAEP

Заключение

Т.е. RSA это не только возведение в степень по модулю большого числа. Это еще и добавление избыточных данных позволяющих реализовать дополнительную защиту вашей информации. Вы, возможно, спросите: а зачем это все нужно? Неужели в действительности может произойти такая ситуация, когда атакующий получит доступ к расшифровывающему алгоритму? Совсем по другому поводу как-то было сказано: если какая-либо неприятность может произойти, она обязательно произойдет. Только вот с использованием схем дополнений это уже не будет считаться неприятностью.

upd: перенес в блог криптография.
upd2:
Литература и ссылки:
1. Н. Фергюссон, Б. Шнайер «Практическая криптография»
2. Н. Смарт «Криптография»
3. Спецификация RSA-OAEP(pdf)

Источник

RSA: от простых чисел до электронной подписи

Выясняем, как и откуда можно получить электронную подпись на примере криптосистемы RSA.

Содержание

Определения и обозначения

Описание криптосистемы RSA

Асимметричные криптографические системы

Шифрование и дешифрование

Получение подписи сообщения по RSA

Электронная подпись документов

Введение

Наверняка вы сталкивались с таким понятием, как «электронная подпись». Если обратиться к федеральному закону, то можно найти следующее её определение:

Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2012, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.

Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.

Теорминимум

Сформируем небольшой словарик терминов, которые нам пригодятся далее:

Открытый текст – данные, подлежащие шифрованию или полученные в результате расшифрования

Шифртекст – данные, полученные в результате применения шифра к открытому тексту

Шифр – совокупность обратимых преобразований, зависящая от некоторого параметра (ключа)

Ключ – параметр шифра, определяющий выбор одного преобразования из совокупности.

Факторизация – процесс разложения числа на простые множители.

НОД – наибольший общий делитель.

Числа a и b называются взаимно простыми, если НОД этих чисел равен 1.

Функция Эйлера φ(n) – функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним.

Хочу отметить, что на данном этапе подразумевается, что вы знакомы с арифметическими операциями по модулю. Если нет, то здесь можно о них почитать.

Как оно устроено

Прежде, чем окунуться в необъятный мир математики рассмотреть, как именно устроена RSA, обратимся к тому, как работают

Асимметричные криптосистемы

Рассмотрим задачу сохранности содержимого посылки при передаче от отправителя к адресату. Вот картинка с многим полюбившимся Алисой и Бобом:

Алиса хочет передать Бобу посылку. Для начала Боб на своей стороне создает уникальные замок и ключ к нему (открытый и закрытый ключ соответственно). Далее, Боб делится с окружающим миром своим замком, чтобы любой желающий отправить ему посылку смог её закрыть. Поскольку ключ от подобного замка один и находится только у Боба, никто, кроме Боба, просмотреть содержимое после защёлкивания замка не сможет. В конце концов, Алиса с помощью полученного замка закрывает посылку и передаёт Бобу, который открывает её своим ключом. Таким образом устроены асимметричные криптографические системы, которой как раз является RSA.

В схеме передачи посылки все объекты вполне материальны. Однако сообщения, которые мы хотим шифровать, являются ничем иным, как последовательностью бит, которую нельзя «закрыть» на физический замок. Таким образом возникают вопросы: что такое ключ и замок? Как Бобу создать ключи? Каким образом ключи связаны и как с их помощью зашифровать сообщение? Здесь нам поможет математика.

Теперь к математике

Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция я y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно. Аналогично, односторонней функцией с секретом называется функция y=f(x, k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.

Подобным свойством обладает операция возведения числа в степень по модулю:

Здесь φ(n) – функция Эйлера числа n. Пока условимся, что это работает, далее это будет доказано более строго. Теперь нужно понять, что из это является ключами Боба, а что сообщением. В нашем распоряжении имеются числа c, m, n, e, d.

Давайте посмотрим на первое выражение. Здесь число c получено в результате возведения в степень по модулю числа m. Назовём это действие шифрованием. Тогда становится очевидно, что m выступает в роли открытого текста, а c – шифртекста. Результат c зависит от степени e, в которую мы возводим m, и от модуля n, по которому мы получаем результат шифрования. Эту пару чисел (e, n) мы будем называть открытым ключом. Им Алиса будет шифровать сообщение.

Смотрим на второе действие. Здесь d является параметром, с помощью которого мы получаем исходный текст m из шифртекста c. Этот параметр мы назовём закрытым ключом и выдадим его Бобу, чтобы он смог расшифровать сообщение Алисы.

Что есть что разобрались, теперь перейдём к конкретике, а именно – генерации ключей Боба. Давайте выберем число n такое, что:

где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид:

Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является вычислительно сложной задачей, ровно как и нахождение обратного элемента по модулю. Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).

Возвращаемся к генерации ключей. Выберем целое число e:

Для него вычислим число d:

Для отыскания числа, обратного по модулю, можно воспользоваться алгоритмом Евклида.

Мы завершили с этапом генерации ключей. Теперь Боб публикует свой открытый ключ (e, n), прячет закрытый d, а мы переходим к Алисе.

Шифруем, дешифруем.

Возьмём в качестве сообщения число m (m ∈ [1, n − 1]). Чтобы Алисе зашифровать его, необходимо возвести его в степень e по модулю n. Эти числа идут вместе с открытым ключом Боба:

Здесь за с обозначен шифртекст, который Алиса будет должна передать Бобу. Отметим также, что c ∈ [1, n − 1], как и m. Расшифруем шифртекст, возведя его в степень закрытого ключа Боба d:

Здесь нам понадобится теорема Эйлера:

Также полезной будет китайская теорема об остатках:

Получаем подпись сообщения

Ещё раз напишем две ключевые формулы шифрования и расшифрования соответственно:

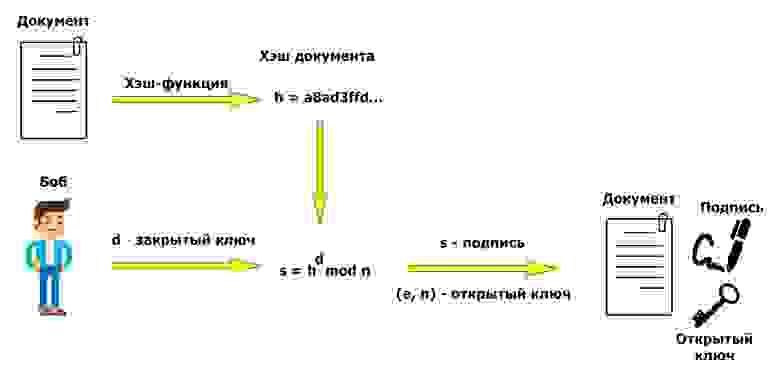
Теперь давайте предположим, что Боб хочет отправить Алисе открытку m от своего имени. У Боба в распоряжении уже имеются два ключа (e, n) и d, которые он сгенерировал по алгоритму, описанному ранее. Поскольку d является закрытым ключом, то можно им воспользоваться как уникальным идентификатором Боба. Давайте «зашифруем» m с помощью d:

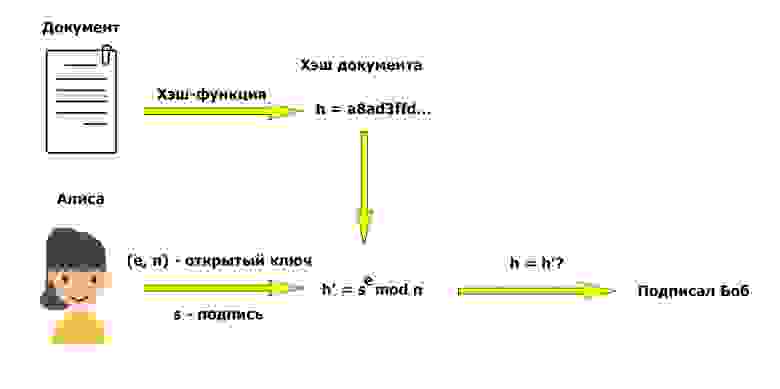
Результат данной операции и есть подпись сообщения Боба. Заметим, что подпись напрямую зависит от подписываемого сообщения, а не только от того, что его подписывает Боб. Далее, Алиса получает сообщение m, подпись s и открытый ключ (e, n). По аналогии с расшифрованием, проверка подписи осуществляется возведением подписи s в степень открытой экспоненты e:

Если Алиса получила, что m ≡ m′, то подпись считается правильной.

Дочитавших до этого места хочу поздравить с получением первой цифровой подписи «на бумаге»!

Подпись документов

Рассмотренный алгоритм получения подписи изящен и прост в осознании, однако операция возведения в степень несколько «мешается». Наша текущая задача – подписать объёмный документ. Чтобы сэкономить время, мы не будем подписывать содержимое документа, а прибегнем к помощи хэш-функций (если вы не знаете, что такое хэш-функция, рекомендую почитать википедию). Скажу лишь то, что выходная последовательность хэш-функции имеет небольшую (по сравнению с размером ключей) длину, а также по имеющемуся хэшу нельзя однозначно восстановить исходные данные.

На картинках наглядно показано, в какой момент мы используем хэширование. Создание подписи:

В качестве хэш-функции можно использовать SHA-256, как это сделано, например, в PGP. По теме практического создания электронной подписи с использованием PGP на хабре уже написана статья, поэтому на этом месте имеет смысл поставить точку и перейти к заключению.

Заключение

Вот мы и прошли все стадии создания электронной подписи, начиная с простой модульной арифметики и заканчивая, собственно, получением подписи. Обладая этими знаниями, вы можете попробовать перевести их на ваш любимый язык программирования и написать свою защищенную аську, например. В том, как именно их применить, вас ограничит только ваше воображение.

Отмечу, что другие существующие алгоритмы создания ЭП основаны на схожих принципах, поэтому надеюсь, что после прочтения этой статьи вам будет проще разобраться в них. «Следующей по сложности» я обозначу криптосистему Эль-Гамаля, но о ней уже не в этом посте.

Спасибо за внимание!

Источники

Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone

Криптографические методы защиты информации: учеб. пособие / С. М. Владимиров, Э. М. Габидулин, А. И. Колыбельников, А. С. Кшевецкий; под ред. А. В. Уривского. – М.: МФТИ, 2016

Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006.

NIST Special Publication 800-57 Part 3 Revision 1

Источник