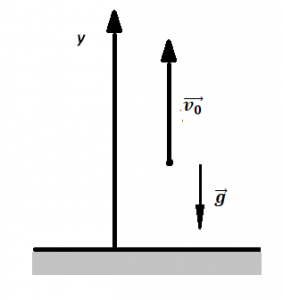
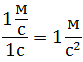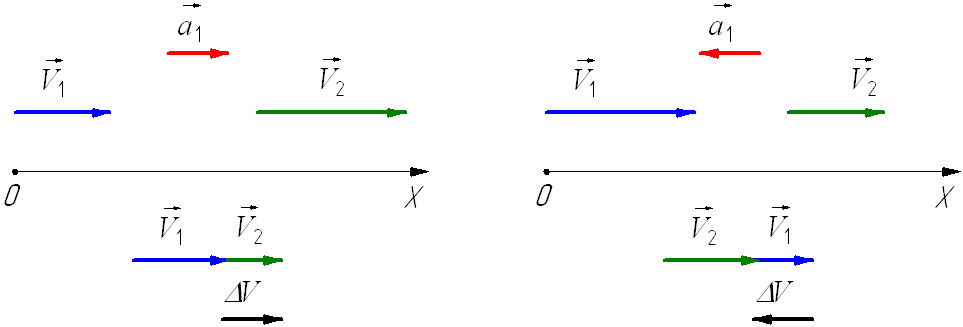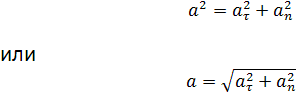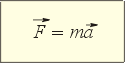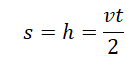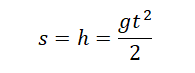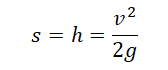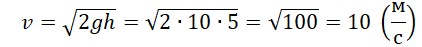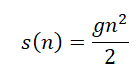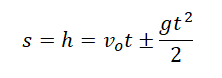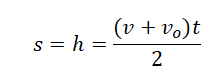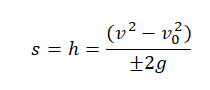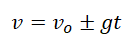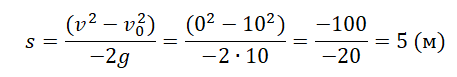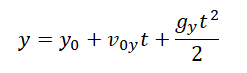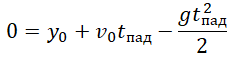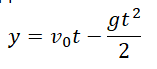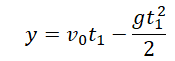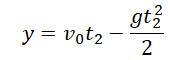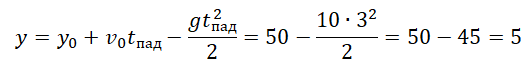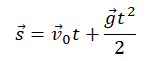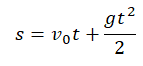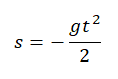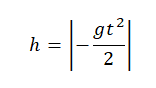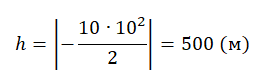С чем сонаправлено ускорение
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 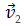
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
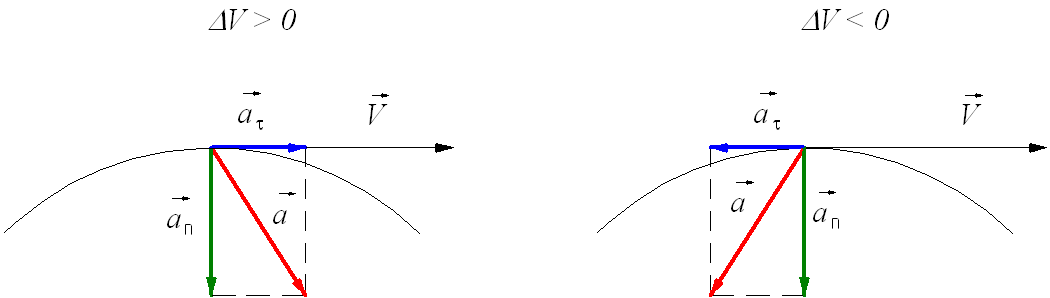
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 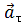
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 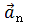
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Физика
А Вы уже инвестируете?
Слышали про акцию в подарок?
Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб
План урока:
Закон сложения скоростей
Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью относительно земли. Это будет собственная скорость пчелы. Затем погода меняется и начинает дуть ветер, перпендикулярный скорости пчелы. Скорость ветра обозначена (см. рисунок 1).
Рисунок 1 – Первоначальная скорость пчелы и ветра
Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):
Рисунок 2 – Изменившаяся скорость пчелы
Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v2 системе отсчета.
Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре
Мгновенная скорость, направление мгновенной скорости
Средняя скорость. Средняя путевая скорость
Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.
Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.
Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:
Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.
То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.
Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt1, Δt2,…Δtn, и найти средние скорости за эти отрезки времени:
А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δtb направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.
Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:
Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.
Ускорение. Касательное ускорение. Центростремительное ускорение
Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.
Единицы измерения ускорения:
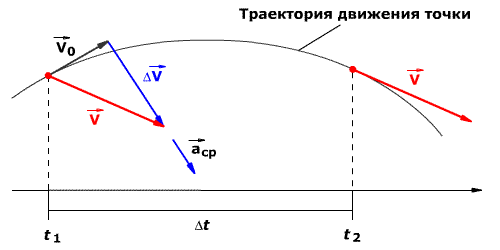
Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)
Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.
Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).
Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2
Равноускоренное движение
Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении
Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:
Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.
При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:
Если же ускорение противонаправлено начальной скорости, это выражение станет таким:
Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении
Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.
Свободное падение
Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение
Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.
Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).
Рисунок 9 – Свободное падение тела
Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:
Представим, что тело подкинули вертикально наверх с начальной скоростью v0 (см. рисунок 10).
Рисунок 10 – Тело бросили вертикально вверх
Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v0 (вообще нужно было бы писать voy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).
Отсюда можно найти полное время полета:
Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью под углом α к горизонту.
Рисунок 11 – Тело брошено под углом к горизонту
Уравнения движения в общем виде по двум осям выглядят так:
Еще время полета можно посчитать, учитывая что в двух моментах – в начале полета и в конце. Значит можно посчитать:
Равномерное движение точки по окружности
Центростремительное ускорение
Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).
Рисунок 12 – Изменение направления скорости при равномерном движении по окружности
За изменение направления скорости отвечает центростремительное ускорение ( Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:
где R – радиус окружности, по которой циклически движется тело.
Второй закон Ньютона
Сила – физическая величина, измеряемоя прибором динамометром и характеризующей действие одного тела на другое. Если на тело действует неуравновешенная сила, то такое тело обязательно изменяет свою скорость или направление движения. Другими словами, действие на тело неуравновешенной силы приводит к появлению ускорения.
Возникает вопрос: каким образом сила и вызываемое ей ускорение связаны друг с другом? Какова формула, выражающая связь этих величин?
Ответ на этот вопрос дает второй закон Ньютона: вектор силы, действующей на тело, в инерциальной системе отсчета равен произведению массы на вектор ускорения этого тела.
Чтобы убедиться в справедливости этой формулы, нужно измерить величины F и ma по отдельности, а затем сравнить их численные значения и направления векторов. Сделаем это. Возьмем прибор, представляющий из себя легко вращающийся диск (1). На нем укреплены указатель частоты вращения (2) и толстая линейка (3), одновременно служащая «рельсом» для ролика (4). При помощи нити ролик привязан к динамометру (5). При вращении ролик натянет нить, и динамометр покажет некую силу F, тем бо’льшую, чем быстрее вращается диск.
Вращая диск, мы получим, например, такие данные:
| Ролик массой 0,25 кг | Ролик массой 0,5 кг | |||
| радиус (R), м | 0.2 | 0.2 | 0.2 | 0.2 |
| период (T), с | 1 | 2 | 1 | 2 |
| ускорение (а) | » 8 м/с2 | » 2 м/с2 | » 8 м/с2 | » 4 м/с2 |
| сила (F) | »2 H | »0.5 H | »4 H | »1 H |
Рассмотрим, как получились эти числа. Радиус R – это расстояние от ролика до центра диска. Во время вращения диска ролик откатывается по линейке до отметки 20 см. Значит, R = 0.2 м. Период T – это время, за которое диск совершает один оборот. Указатель частоты вращения на рисунке показывает 1 об/с. То есть за секунду совершается один оборот. Следовательно, период T = 1 с. Вычисляя центростремительное ускорение ролика по формуле a = 4p2R/T2, получим: 4 · 3.142 · 0.2 / 12 » 8 м/с2. Именно это число и записано в клетке «ускорение».
Итак, справедливо ли равенство F=ma? Перемножим подчеркнутые числа верхней таблицы. Имеем: 2 Н » 0.25 кг · 8 м/с2. Другими словами, F » ma.
Теперь убедимся, что векторы F и ma сонаправлены. Вспомним, что вектор центростремительного ускорения тела при его равномерном движении по окружности всегда направлен к центру этой окружности. Выясним, куда направлен вектор силы, придающей ролику это ускорение. Вообразим на мгновение, что нить, связывающая ролик и динамометр, вдруг оборвалась. Что произойдет с роликом? Он покатится по линейке и соскочит с диска. Следовательно, нить тянула ролик к оси вращения, не позволяя ему откатиться дальше. Другими словами, вектор F сонаправлен с вектором ускорения.
Таким образом мы подтвердили истинность векторного равенства: F = ma.
Движение тела с ускорением свободного падения
теория по физике 🧲 кинематика
Свободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
Формула определения перемещения тела в n-ную секунду свободного падения:
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.
Движение тела, брошенного вертикально вверх
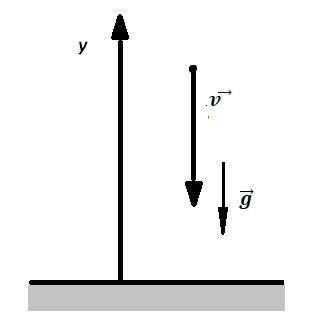
Движение тела, брошенного вертикально вверх, описывается в два этапа
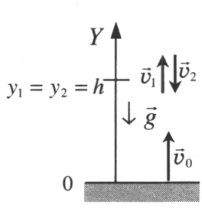
Два этапа движения тела, брошенного вертикально вверх Этап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях ( v ↑↓ g ). Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону ( v ↑↑ g ). Формулы для расчета параметров движения тела, брошенного вертикально вверх Перемещение тела, брошенного вертикально вверх, определяется по формуле:
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
Если время движения неизвестно, для определения перемещения используется следующая формула:
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
Уравнение скорости при свободном падении:
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
Свободное падение на землю с некоторой высоты
Тело подбросили от земли и поймали на некоторой высоте
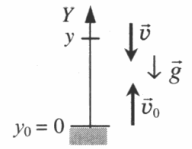
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Интервал времени между моментами прохождения высоты h:
Уравнение координаты для первого прохождения h:
Уравнение координаты для второго прохождения h:
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Через 3 с после падения тело окажется на высоте 5 м.
Алгоритм решения
Решение
Записываем исходные данные:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу для определения скорости тела в векторном виде:
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
Подставим известные данные и вычислим скорость:
pазбирался: Алиса Никитина | обсудить разбор | оценить